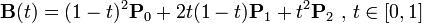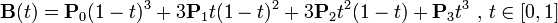38 | CSS动画与交互：为什么动画要用贝塞尔曲线这么奇怪的东西？

你好，我是 winter，今天我们来学习一下 CSS 的动画和交互。

在 CSS 属性中，有这么一类属性，它负责的不是静态的展现，而是根据用户行为产生交互。这就是今天我们要讲的属性。

首先我们先从属性来讲起。CSS 中跟动画相关的属性有两个：animation 和 transition。

animation 属性和 transition 属性

我们先来看下 animation 的示例，通过示例来了解一下 animation 属性的基本用法:

@keyframes mykf
{
  from {background: red;}
  to {background: yellow;}
}
 
div
{
    animation:mykf 5s infinite;
}
复制代码

这里展示了 animation 的基本用法，实际上 animation 分成六个部分：

• animation-name 动画的名称，这是一个 keyframes 类型的值（我们在第 9 讲“CSS 语法：除了属性和选择器，你还需要知道这些带 @的规则”讲到过，keyframes 产生一种数据，用于定义动画关键帧）；
• animation-duration 动画的时长；
• animation-timing-function 动画的时间曲线；
• animation-delay 动画开始前的延迟；
• animation-iteration-count 动画的播放次数；
• animation-direction 动画的方向。

我们先来看 animation-name

比如，我们前面的示例中，就必须配合定义 mymove 这个 keyframes。keyframes 的主体结构是一个名称和花括号中的定义，它按照百分比来规定数值，例如：

@keyframes mykf {
  0% { top: 0; }
  50% { top: 30px; }
  75% { top: 10px; }
  100% { top: 0; }
}
复制代码

这里我们可以规定在开始时把 top 值设为 0，在 50% 是设为 30px，在 75% 时设为 10px，到 100% 时重新设为 0，这样，动画执行时就会按照我们指定的关键帧来变换数值。

这里，0% 和 100% 可以写成 from 和 to，不过一般不会混用，画风会变得很奇怪，比如：

@keyframes mykf {
  from { top: 0; }
  50% { top: 30px; }
  75% { top: 10px; }
  to { top: 0; }
}
复制代码

这里关键帧之间，是使用 animation-timing-function

接下来我们来介绍一下 transition。transition 与 animation 相比来说，是简单得多的一个属性。

它有四个部分：

• transition-property 要变换的属性；
• transition-duration 变换的时长；
• transition-timing-function 时间曲线；
• transition-delay 延迟。

这里的四个部分，可以重复多次，指定多个属性的变换规则。

实际上，有时候我们会把 transition 和 animation 组合，抛弃 animation 的 timing-function，以编排不同段用不同的曲线。

@keyframes mykf {
  from { top: 0; transition:top ease}
  50% { top: 30px;transition:top ease-in }
  75% { top: 10px;transition:top ease-out }
  to { top: 0; transition:top linear}
}
复制代码

在这个例子中，在 keyframes 中定义了 transition 属性，以达到各段曲线都不同的效果。

接下来，我们就来详细讲讲刚才提到的 timing-function，动画的时间曲线。

三次贝塞尔曲线

我想，你能从很多 CSS 的资料中都找到了贝塞尔曲线，但是为什么 CSS 的时间曲线要选用（三次）贝塞尔曲线呢？

我们在这里首先要了解一下贝塞尔曲线，贝塞尔曲线是一种插值曲线，它描述了两个点之间差值来形成连续的曲线形状的规则。

一个量（可以是任何矢量或者标量）从一个值到变化到另一个值，如果我们希望它按照一定时间平滑地过渡，就必须要对它进行插值。

最基本的情况，我们认为这个变化是按照时间均匀进行的，这个时候，我们称其为线性插值。而实际上，线性插值不大能满足我们的需要，因此数学上出现了很多其它的插值算法，其中贝塞尔插值法是非常典型的一种。它根据一些变换中的控制点来决定值与时间的关系。

贝塞尔曲线是一种被工业生产验证了很多年的曲线，它最大的特点就是“平滑”。时间曲线平滑，意味着较少突兀的变化，这是一般动画设计所追求的。

贝塞尔曲线用于建筑设计和工业设计都有很多年历史了，它最初的应用是汽车工业用贝塞尔曲线来设计车型。

K 次贝塞尔插值算法需要 k+1 个控制点，最简单的一次贝塞尔插值就是线性插值，将时间表示为 0 到 1 的区间，一次贝塞尔插值公式是：

“二次贝塞尔插值”有 3 个控制点，相当于对 P0 和 P1，P1 和 P2 分别做贝塞尔插值，再对结果做一次贝塞尔插值计算

“三次贝塞尔插值”则是“两次‘二次贝塞尔插值’的结果，再做一次贝塞尔插值”：

贝塞尔曲线的定义中带有一个参数 t，但是这个 t 并非真正的时间，实际上贝塞尔曲线的一个点 (x, y)，这里的 x 轴才代表时间。

这就造成了一个问题，如果我们使用贝塞尔曲线的直接定义，是没办法直接根据时间来计算出数值的，因此，浏览器中一般都采用了数值算法，其中公认做有效的是牛顿积分，我们可以看下 JavaScript 版本的代码：

function generate(p1x, p1y, p2x, p2y) {
    const ZERO_LIMIT = 1e-6;
    // Calculate the polynomial coefficients,
    // implicit first and last control points are (0,0) and (1,1).
    const ax = 3 * p1x - 3 * p2x + 1;
    const bx = 3 * p2x - 6 * p1x;
    const cx = 3 * p1x;
 
    const ay = 3 * p1y - 3 * p2y + 1;
    const by = 3 * p2y - 6 * p1y;
    const cy = 3 * p1y;
 
    function sampleCurveDerivativeX(t) {
        // `ax t^3 + bx t^2 + cx t' expanded using Horner 's rule.
        return (3 * ax * t + 2 * bx) * t + cx;
    }
 
    function sampleCurveX(t) {
        return ((ax * t + bx) * t + cx ) * t;
    }
 
    function sampleCurveY(t) {
        return ((ay * t + by) * t + cy ) * t;
    }
 
    // Given an x value, find a parametric value it came from.
    function solveCurveX(x) {
        var t2 = x;
        var derivative;
        var x2;
 
        // https://trac.webkit.org/browser/trunk/Source/WebCore/platform/animation
        // First try a few iterations of Newton's method -- normally very fast.
        // http://en.wikipedia.org/wiki/Newton's_method
        for (let i = 0; i < 8; i++) {
            // f(t)-x=0
            x2 = sampleCurveX(t2) - x;
            if (Math.abs(x2) < ZERO_LIMIT) {
                return t2;
            }
            derivative = sampleCurveDerivativeX(t2);
            // == 0, failure
            /* istanbul ignore if */
            if (Math.abs(derivative) < ZERO_LIMIT) {
                break;
            }
            t2 -= x2 / derivative;
        }
 
        // Fall back to the bisection method for reliability.
        // bisection
        // http://en.wikipedia.org/wiki/Bisection_method
        var t1 = 1;
        /* istanbul ignore next */
        var t0 = 0;
 
        /* istanbul ignore next */
        t2 = x;
        /* istanbul ignore next */
        while (t1 > t0) {
            x2 = sampleCurveX(t2) - x;
            if (Math.abs(x2) < ZERO_LIMIT) {
                return t2;
            }
            if (x2 > 0) {
                t1 = t2;
            } else {
                t0 = t2;
            }
            t2 = (t1 + t0) / 2;
        }
 
        // Failure
        return t2;
    }
 
    function solve(x) {
        return sampleCurveY(solveCurveX(x));
    }
 
    return solve;
}
 
复制代码

这段代码其实完全翻译自 WebKit 的 C++ 代码，牛顿积分的具体原理请参考相关数学著作，注释中也有相关的链接。

这个 JavaScript 版本的三次贝塞尔曲线可以用于实现跟 CSS 一模一样的动画。

贝塞尔曲线拟合

理论上，贝塞尔曲线可以通过分段的方式拟合任意曲线，但是有一些特殊的曲线，是可以用贝塞尔曲线完美拟合的，比如抛物线。

这里我做了一个示例，用于模拟抛物线：

<!DOCTYPE html>
<html>
<head>
  <meta charset="utf-8">
  <meta name="viewport" content="width=device-width">
  <title>Simulation</title>
  <style>
    .ball {
      width:10px;
      height:10px;
      background-color:black;
      border-radius:5px;
      position:absolute;
      left:0;
      top:0;
      transform:translateY(180px);
    }
  </style>
</head>
<body>
  <label> 运动时间：<input value="3.6" type="number" id="t" />s</label><br/>
  <label> 初速度：<input value="-21" type="number" id="vy" /> px/s</label><br/>
  <label> 水平速度：<input value="21" type="number" id="vx" /> px/s</label><br/>
  <label> 重力：<input value="10" type="number" id="g" /> px/s²</label><br/>
  <button onclick="createBall()"> 来一个球 </button>
</body>
</html>
复制代码

function generateCubicBezier (v, g, t){
    var a = v / g;
    var b = t + v / g;
 
    return [[(a / 3 + (a + b) / 3 - a) / (b - a), (a * a / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)],
        [(b / 3 + (a + b) / 3 - a) / (b - a), (b * b / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)]];
}
 
function createBall() {
  var ball = document.createElement("div");
  var t = Number(document.getElementById("t").value);
  var vx = Number(document.getElementById("vx").value);
  var vy = Number(document.getElementById("vy").value);
  var g = Number(document.getElementById("g").value);
  ball.className = "ball";
  document.body.appendChild(ball)
  ball.style.transition = `left linear ${t}s, top cubic-bezier(${generateCubicBezier(vy, g, t)}) ${t}s`;
  setTimeout(function(){ 
    ball.style.left = `${vx * t}px`; 
    ball.style.top = `${vy * t + 0.5 * g * t * t}px`; 
  }, 100);
  setTimeout(function(){ document.body.removeChild(ball); }, t * 1000);
}
 
复制代码

这段代码中，我实现了抛物线运动的小球，其中核心代码就是 generateCubicBezier 函数。

这个公式完全来自于一篇论文，推理过程我也不清楚，但是不论如何，它确实能够用于模拟抛物线。

实际上，我们日常工作中，如果需要用贝塞尔曲线拟合任何曲线，都可以找到相应的论文，我们只要取它的结论即可。

总结

我们今天的课程，重点介绍了动画和它背后的一些机制。

CSS 用 transition 和 animation 两个属性来实现动画，这两个属性的基本用法很简单，我们今天还介绍了它们背后的原理：贝塞尔曲线。

我们中介绍了贝塞尔曲线的实现原理和贝塞尔曲线的拟合技巧。

最后，留给你一个小问题，请纯粹用 JavaScript 来实现一个 transition 函数，用它来跟 CSS 的 transition 来做一下对比，看看有哪些区别。