03 | 迭代法：不用编程语言的自带函数，你会如何计算平方根？

你好，我是黄申。

今天我们来说一个和编程结合得非常紧密的数学概念。在解释这个重要的概念之前，我们先来看个有趣的小故事。

古印度国王舍罕酷爱下棋，他打算重赏国际象棋的发明人宰相西萨·班·达依尔。这位聪明的大臣指着象棋盘对国王说：“陛下，我不要别的赏赐，请您在这张棋盘的第一个小格内放入一粒麦子，在第二个小格内放入两粒，第三小格内放入给四粒，以此类推，每一小格内都比前一小格加一倍的麦子，直至放满 64 个格子，然后将棋盘上所有的麦粒都赏给您的仆人我吧！”

国王自以为小事一桩，痛快地答应了。可是，当开始放麦粒之后，国王发现，还没放到第二十格，一袋麦子已经空了。随着，一袋又一袋的麦子被放入棋盘的格子里，国王很快看出来，即便拿来全印度的粮食，也兑现不了对达依尔的诺言。

放满这 64 格到底需要多少粒麦子呢？这是个相当相当大的数字，想要手动算出结果并不容易。如果你觉得自己厉害，可以试着拿笔算算。其实，这整个算麦粒的过程，在数学上，是有对应方法的，这也正是我们今天要讲的概念：迭代法（Iterative Method）。

到底什么是迭代法？

迭代法，简单来说，其实就是不断地用旧的变量值，递推计算新的变量值。

我这么说可能还是比较抽象，不容易理解。我们还回到刚才的故事。大臣要求每一格的麦子都是前一格的两倍，那么前一格里麦子的数量就是旧的变量值，我们可以先记作 ；而当前格子里麦子的数量就是新的变量值，我们记作 。这两个变量的递推关系就是这样的：

如果你稍微有点编程经验，应该能发现，迭代法的思想，很容易通过计算机语言中的循环语言来实现。你知道，计算机本身就适合做重复性的工作，我们可以通过循环语句，让计算机重复执行迭代中的递推步骤，然后推导出变量的最终值。

那接下来，我们就用循环语句来算算，填满格子到底需要多少粒麦子。我简单用 Java 语言写了个程序，你可以看看。

public class Lesson3_1 {
    /**
    * @Description: 算算舍罕王给了多少粒麦子
    * @param grid- 放到第几格
    * @return long- 麦粒的总数
    */
 
    public static long getNumberOfWheat(int grid) {
     
     long sum = 0;      // 麦粒总数
     long numberOfWheatInGrid = 0;  // 当前格子里麦粒的数量
     
     numberOfWheatInGrid = 1;  // 第一个格子里麦粒的数量
     sum += numberOfWheatInGrid;  
     
     for (int i = 2; i <= grid; i ++) {
      numberOfWheatInGrid *= 2;   // 当前格子里麦粒的数量是前一格的 2 倍
      sum += numberOfWheatInGrid;   // 累计麦粒总数
     }
     
     return sum;
 
    }
}
复制代码

下面是一段测试代码，它计算了到第 63 格时，总共需要多少麦粒。

  public static void main(String[] args) {
  System.out.println(String.format(" 舍罕王给了这么多粒：%d",   Lesson3_1.getNumberOfWheat(63)));
  }
复制代码

计算的结果是 9223372036854775807，多到数不清了。我大致估算了一下，一袋 50 斤的麦子估计有 130 万粒麦子，那么 9223372036854775807 相当于 70949 亿袋 50 斤的麦子！

这段代码有两个地方需要注意。首先，用于计算每格麦粒数的变量以及总麦粒数的变量都是 Java 中的 long 型，这是因为计算的结果实在是太大了，超出了 Java int 型的范围；第二，我们只计算到了第 63 格，这是因为计算到第 64 格之后，总数已经超过 Java 中 long 型的范围。

迭代法有什么具体应用？

看到这里，你可能大概已经理解迭代法的核心理念了。迭代法在无论是在数学，还是计算机领域都有很广泛的应用。大体上，迭代法可以运用在以下几个方面：

• 求数值的精确或者近似解。典型的方法包括二分法（Bisection method）和牛顿迭代法（Newton’s method）。

• 在一定范围内查找目标值。典型的方法包括二分查找。

• 机器学习算法中的迭代。相关的算法或者模型有很多，比如 K- 均值算法（K-means clustering）、PageRank 的马尔科夫链（Markov chain）、梯度下降法（Gradient descent）等等。迭代法之所以在机器学习中有广泛的应用，是因为很多时候机器学习的过程，就是根据已知的数据和一定的假设，求一个局部最优解。而迭代法可以帮助学习算法逐步搜索，直至发现这种解。

这里，我详细讲解一下求数值的解和查找匹配记录这两个应用。

1. 求方程的精确或者近似解

迭代法在数学和编程的应用有很多，如果只能用来计算庞大的数字，那就太“暴殄天物”了。迭代还可以帮助我们进行无穷次地逼近，求得方程的精确或者近似解。

比如说，我们想计算某个给定正整数 n（n>1）的平方根，如果不使用编程语言自带的函数，你会如何来实现呢？

假设有正整数 n，这个平方根一定小于 n 本身，并且大于 1。那么这个问题就转换成，在 1 到 n 之间，找一个数字等于 n 的平方根。

我这里采用迭代中常见的二分法。每次查看区间内的中间值，检验它是否符合标准。

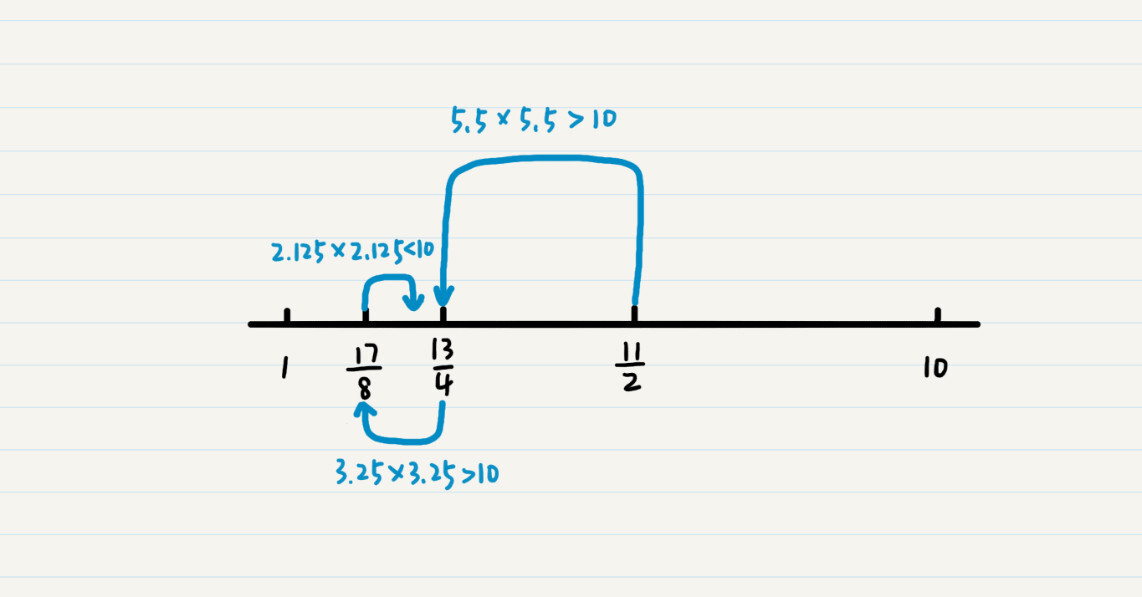
举个例子，假如我们要找到 10 的平方根。我们需要先看 1 到 10 的中间数值，也就是 11/2=5.5。5.5 的平方是大于 10 的，所以我们要一个更小的数值，就看 5.5 和 1 之间的 3.25。由于 3.25 的平方也是大于 10 的，继续查看 3.25 和 1 之间的数值，也就是 2.125。这时，2.125 的平方小于 10 了，所以看 2.125 和 3.25 之间的值，一直继续下去，直到发现某个数的平方正好是 10。

我把具体的步骤画成了一张图，你可以看看。

我这里用 Java 代码演示一下效果，你可以结合上面的讲解，来理解迭代的过程。

public class Lesson3_2 {
 
 /**
    * @Description: 计算大于 1 的正整数之平方根
    * @param n- 待求的数, deltaThreshold- 误差的阈值, maxTry- 二分查找的最大次数
    * @return double- 平方根的解
    */
    public static double getSqureRoot(int n, double deltaThreshold, int maxTry) {
     
     if (n <= 1) {
      return -1.0;
     }
     
     double min = 1.0, max = (double)n;
     for (int i = 0; i < maxTry; i++) {
      double middle = (min + max) / 2;
      double square = middle * middle;
      double delta = Math.abs((square / n) - 1);
      if (delta <= deltaThreshold) {
       return middle;
      } else {
       if (square > n) {
        max = middle;
       } else {
        min = middle;
       }
      }
     }
     
     return -2.0;
 
    }
}
复制代码

这是一段测试代码，我们用它来找正整数 10 的平方根。如果找不到精确解，我们就返回一个近似解。

public static void main(String[] args) {
  
  int number = 10;
  double squareRoot = Lesson3_2.getSqureRoot(number, 0.000001, 10000);
  if (squareRoot == -1.0) {
   System.out.println(" 请输入大于 1 的整数 ");
  } else if (squareRoot == -2.0) {
   System.out.println(" 未能找到解 ");
  } else {
   System.out.println(String.format("%d 的平方根是 %f", number, squareRoot));
  }
  
 }
复制代码

这段代码的实现思想就是我前面讲的迭代过程，这里面有两个小细节我解释下。

第一，我使用了 deltaThreshold 来控制解的精度。虽然理论上来说，可以通过二分的无限次迭代求得精确解，但是考虑到实际应用中耗费的大量时间和计算资源，绝大部分情况下，我们并不需要完全精确的数据。

第二，我使用了 maxTry 来控制循环的次数。之所以没有使用 while(true) 循环，是为了避免死循环。虽然，在这里使用 deltaThreshold，理论上是不会陷入死循环的，但是出于良好的编程习惯，我们还是尽量避免产生的可能性。

说完了二分迭代法，我这里再简单提一下牛顿迭代法。这是牛顿在 17 世纪提出的一种方法，用于求方程的近似解。这种方法以微分为基础，每次迭代的时候，它都会去找到比上一个值 更接近的方程的根，最终找到近似解。该方法及其延伸也被应用在机器学习的算法中，在之后机器学习中的应用中，我会具体介绍这个算法。

2. 查找匹配记录

二分法中的迭代式逼近，不仅可以帮我们求得近似解，还可以帮助我们查找匹配的记录。我这里用一个查字典的案例来说明。

在自然语言处理中，我们经常要处理同义词或者近义词的扩展。这时，你手头上会有一个同义词 / 近义词的词典。对于一个待查找的单词，我们需要在字典中找出这个单词，以及它所对应的同义词和近义词，然后进行扩展。比如说，这个字典里有一个关于“西红柿”的词条，其同义词包括了“番茄”和“tomato”。

那么，在处理文章的时候，当我们看到了“西红柿”这个词，就去字典里查一把，拿出“番茄”“tomato”等等，并添加到文章中作为同义词 / 近义词的扩展。这样的话，用户在搜索“西红柿”这个词的时候，我们就能确保出现“番茄”或者“tomato”的文章会被返回给用户。

乍一看到这个任务的时候，你也许想到了哈希表。没错，哈希表是个好方法。不过，如果不使用哈希表，你还有什么其他方法呢？这里，我来介绍一下，用二分查找法进行字典查询的思路。

第一步，将整个字典先进行排序（假设从小到大）。二分法中很关键的前提条件是，所查找的区间是有序的。这样才能在每次折半的时候，确定被查找的对象属于左半边还是右半边。

第二步，使用二分法逐步定位到被查找的单词。每次迭代的时候，都找到被搜索区间的中间点，看看这个点上的单词，是否和待查单词一致。如果一致就返回；如果不一致，要看被查单词比中间点上的单词是小还是大。如果小，那说明被查的单词如果存在字典中，那一定在左半边；否则就在右半边。

第三步，根据第二步的判断，选择左半边或者后半边，继续迭代式地查找，直到范围缩小到单个的词。如果到最终仍然无法找到，则返回不存在。

当然，你也可以对单词进行从大到小的排序，如果是那样，在第二步的判断就需要相应地修改一下。

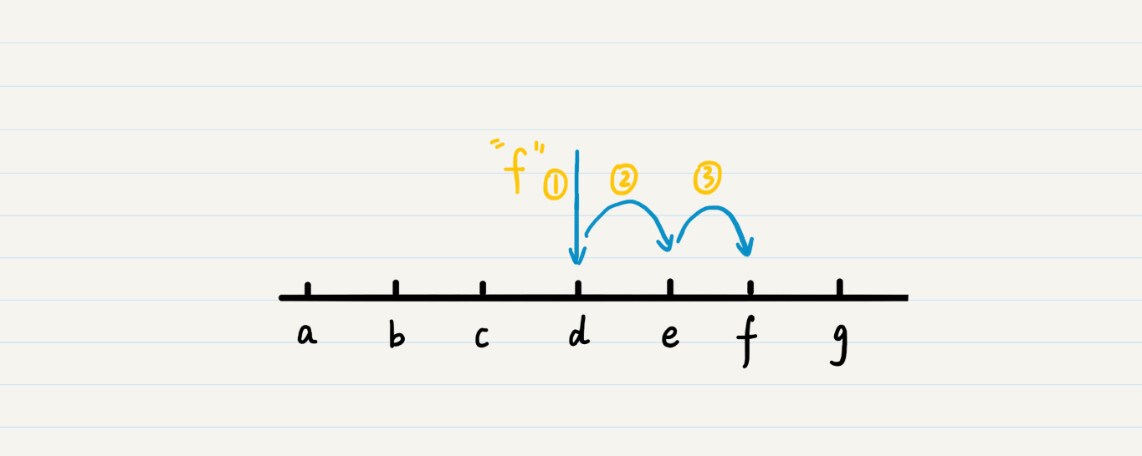
我把在 a 到 g 的 7 个字符中查找 f 的过程，画成了一张图，你可以看看。

这个方法的整体思路和二分法求解平方根是一致的，主要区别有两个方面：第一，每次判断是否终结迭代的条件不同。求平方根的时候，我们需要判断某个数的平方是否和输入的数据一致。而这里，我们需要判断字典中某个单词是否和待查的单词相同。第二，二分查找需要确保被搜索的空间是有序的。

我把具体的代码写出来了，你可以看一下。

import java.util.Arrays;
 
public class Lesson3_3 {
 
 /**
    * @Description: 查找某个单词是否在字典里出现
    * @param dictionary- 排序后的字典, wordToFind- 待查的单词
    * @return boolean- 是否发现待查的单词
    */
    public static boolean search(String[] dictionary, String wordToFind) {
     
     if (dictionary == null) {
      return false;
     }
     
     if (dictionary.length == 0) {
      return false;
     }
     
     int left = 0, right = dictionary.length - 1;
     while (left <= right) {
      int middle = (left + right) / 2;
      if (dictionary[middle].equals(wordToFind)) {
       return true;
      } else {
       if (dictionary[middle].compareTo(wordToFind) > 0) {
        right = middle - 1;
       } else {
        left = middle + 1;
       }
      }
     }
     
     return false;
 
    }
 
}
 
 
复制代码

我测试代码首先建立了一个非常简单的字典，然后使用二分查找法在这个字典中查找单词“i”。

public static void main(String[] args) {
  
  
  String[] dictionary = {"i", "am", "one", "of", "the", "authors", "in", "geekbang"};
  
  Arrays.sort(dictionary);
 
  String wordToFind = "i";
  
  boolean found = Lesson3_3.search(dictionary, wordToFind);
  if (found) {
   System.out.println(String.format(" 找到了单词 %s", wordToFind));
  } else {
   System.out.println(String.format(" 未能找到单词 %s", wordToFind));
  }
  
 }
复制代码

说的这两个例子，都属于迭代法中的二分法，我在第一节的时候说过，二分法其实也体现了二进制的思想。

小结

到这里，我想你对迭代的核心思路有了比较深入的理解。

实际上，人类并不擅长重复性的劳动，而计算机却很适合做这种事。这也是为什么，以重复为特点的迭代法在编程中有着广泛的应用。不过，日常的实际项目可能并没有体现出明显的重复性，以至于让我们很容易就忽视了迭代法的使用。所以，你要多观察问题的现象，思考其本质，看看不断更新变量值或者缩小搜索的区间范围，是否可以获得最终的解（或近似解、局部最优解），如果是，那么你就可以尝试迭代法。

思考题

在你曾经做过的项目中，是否使用过迭代法？如果有，你觉得迭代法最大的特点是什么？如果还没用过，你想想看现在的项目中是否有可以使用的地方？

欢迎在留言区交作业，并写下你今天的学习笔记。你可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。