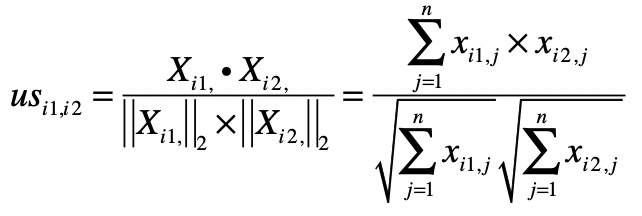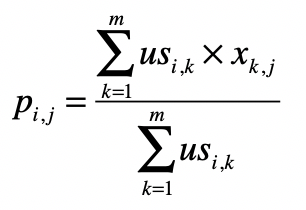38 | 矩阵（下）：如何使用矩阵操作进行协同过滤推荐？

你好，我是黄申。今天我们来聊聊矩阵操作和推荐算法的关系。

我这里说的推荐，是指为用户提供可靠的建议、并协助用户挑选物品的一种技术。一个好的推荐系统需要建立在海量数据挖掘基础之上，并根据用户所处的情景和兴趣特点，向用户推荐可能感兴趣的信息和商品。

协同过滤（Collaborative Filtering）是经典的推荐算法之一，它充分利用了用户和物品之间已知的关系，为用户提供新的推荐内容。我会从这种二元关系出发，给你讲讲如何使用矩阵计算，来实现协同过滤推荐算法。

用矩阵实现推荐系统的核心思想

矩阵中的二维关系，除了可以表达图的邻接关系，还可以表达推荐系统中用户和物品的关系。如果你不懂推荐系统，不用急，我这里先给你简单讲讲它的核心思想。

简单地理解就是，推荐系统会根据用户所处的场景和个人喜好，推荐他们可能感兴趣的信息和商品。比如，你在阅读一部电影的影评时，系统给你推荐了其他“你可能也感兴趣的电影”。可以看出来，推荐系统中至少有 2 个重要的角色：用户和物品。用户是系统的使用者，物品就是将要被推荐的候选对象。

例如，亚马逊网站的顾客就是用户，网站所销售的商品就是物品。需要注意的是，除了用户角色都是现实中的自然人，某些场景下被推荐的物品可能也是现实中的自然人。例如，一个招聘网站会给企业雇主推荐合适的人才，这时候应聘者承担的是物品角色。

而一个好的推荐算法，需要充分挖掘用户和物品之间的关系。我们可以通过矩阵来表示这种二元关系。我这里有一个例子，我们用矩阵 来表示用户对物品喜好程度。

其中第 行是第 个用户的数据，而第 j 列是用户对第 j 格物品的喜好程度。我们用 表示这个数值。这里的喜好程度可以是用户购买商品的次数、对书籍的评分等等。

假设我们用一个 0 到 1 之间的小数表示。有了这种矩阵，我们就可以通过矩阵的操作，充分挖掘用户和物品之间的关系。下面，我会使用经典的协同过滤算法，来讲解矩阵在其中的运用。

在此之前，我们先来看什么是协同过滤。你可以把它理解为最直观的“口口相传”。假设我们愿意接受他人的建议，尤其是很多人都向你建议的时候。其主要思路就是利用已有用户群过去的行为或意见，预测当前用户最可能喜欢哪些东西。根据推荐依据和传播的路径，又可以进一步细分为基于用户的过滤和基于物品的过滤。

基于用户的过滤

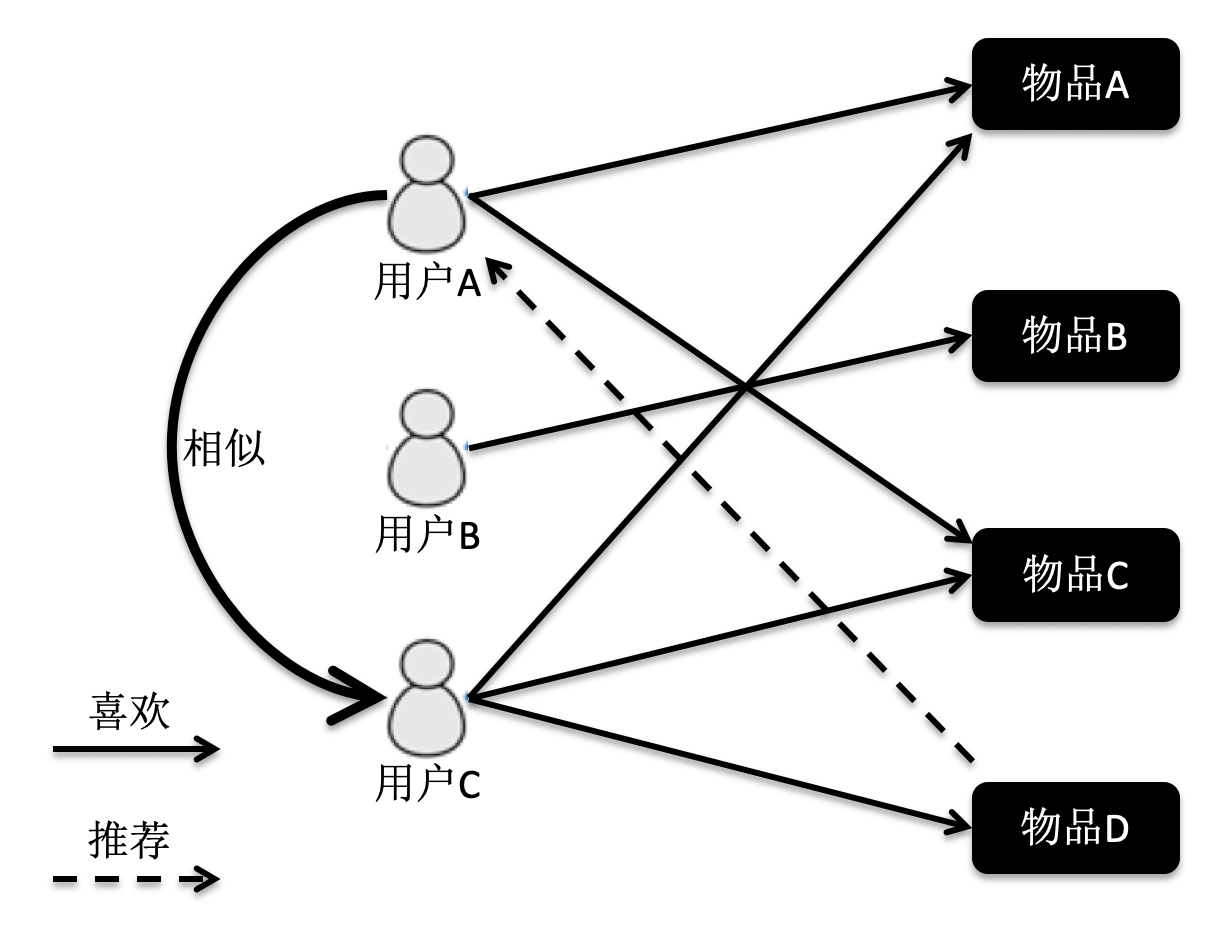
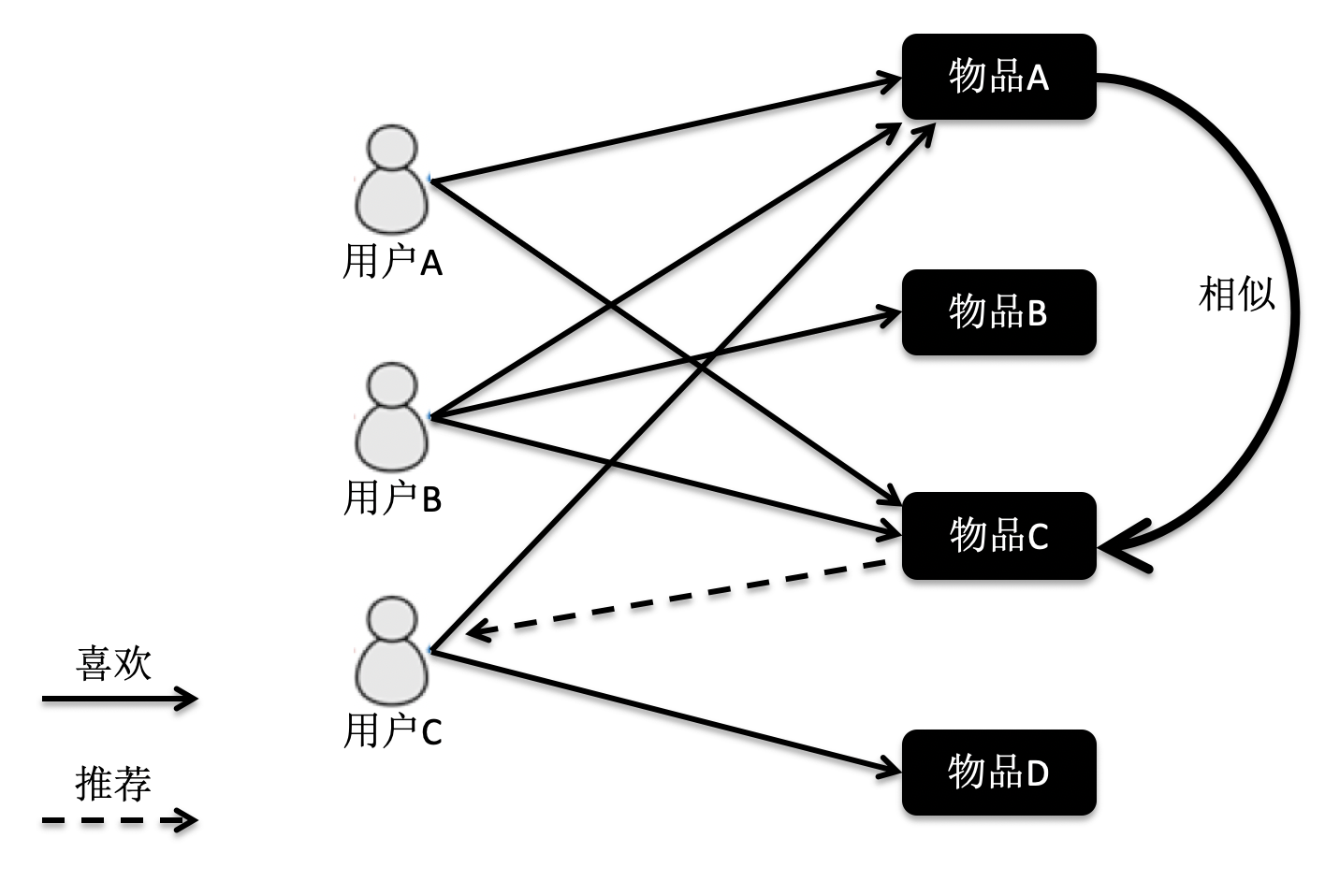
首先，我们来看基于用户的协同过滤。它是指给定一个用户访问（我们假设有访问就表示有兴趣）物品的数据集合，找出和当前用户历史行为有相似偏好的其他用户，将这些用户组成“近邻”，对于当前用户没有访问过的物品，利用其近邻的访问记录来预测。我画了一张图方便你理解。

根据这张图的访问关系来看，用户 A 访问了物品 A 和 C，用户 B 访问了物品 B，用户 C 访问了物品 A，C 和 D。我们计算出来，用户 C 是 A 的近邻，而 B 不是。因此系统会更多地向用户 A 推荐用户 C 访问的物品 D。

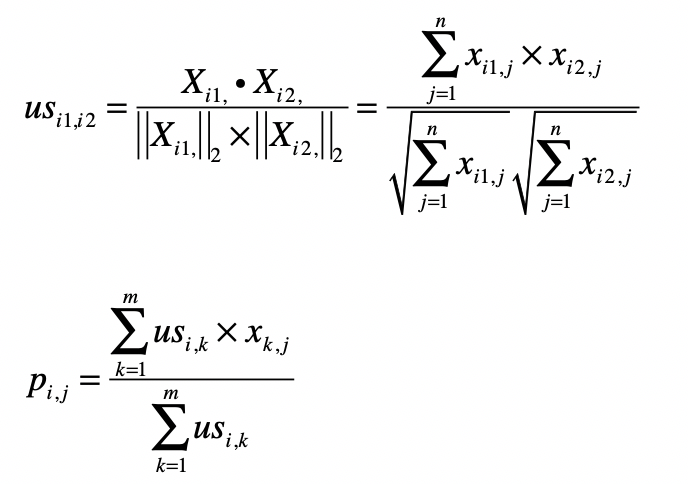
理解了这个算法的基本概念，我们来看看如何使用公式来表述它。假设有 m 个用户，n 个物品，那么我们就能使用一个 m×n 维的矩阵 来表示用户对物品喜好的二元关系。基于这个二元关系，我们可以列出下面这两个公式：

其中，第一个公式比较容易理解，它的核心思想是计算用户和用户之间的相似度。完成了这一步我们就能找到给定用户的“近邻”。

我们可以使用向量空间模型中的距离或者是夹角余弦来处理，在这里我使用了夹角余弦，其中 , 表示用户 和 的相似度，而 , 表示矩阵中第 行的行向量，, 表示矩阵中第 行的行向量。分子是两个表示用户的行向量之点乘，而分母是这两个行向量 范数的乘积。

第二个公式利用第一个公式所计算的用户间相似度，以及用户对物品的喜好度，预测任一个用户对任一个物品的喜好度。其中 表示第 用户对第 个物品的喜好度， 表示用户 和 之间的相似度， 表示用户 对物品 的喜好度。注意这里最终需要除以 ，是为了进行归一化。

从这个公式可以看出，如果 越大， 对最终 的影响越大，反之如果 越小， 对最终 的影响越小，充分体现了“基于相似用户”的推荐。

如果你无法理解如何把这两个公式对应为矩阵操作，没关系，我下面会通过之前介绍的喜好度矩阵 的示例，把这两个公式逐步拆解，并对应到矩阵上的操作，你一看就能明白了。

首先，我们来看第一个关于夹角余弦的公式。

在介绍向量空间模型的时候，我提到夹角余弦可以通过向量的点乘来实现。这对矩阵同样适用，我们可以采用矩阵点乘自身的转置来实现，也就是 。矩阵 的每一行是某个用户的行向量，每个分量表示用户对某个物品的喜好程度。而矩阵 的每一列是某个用户的列向量，每个分量表示用户对某个物品的喜好程度。

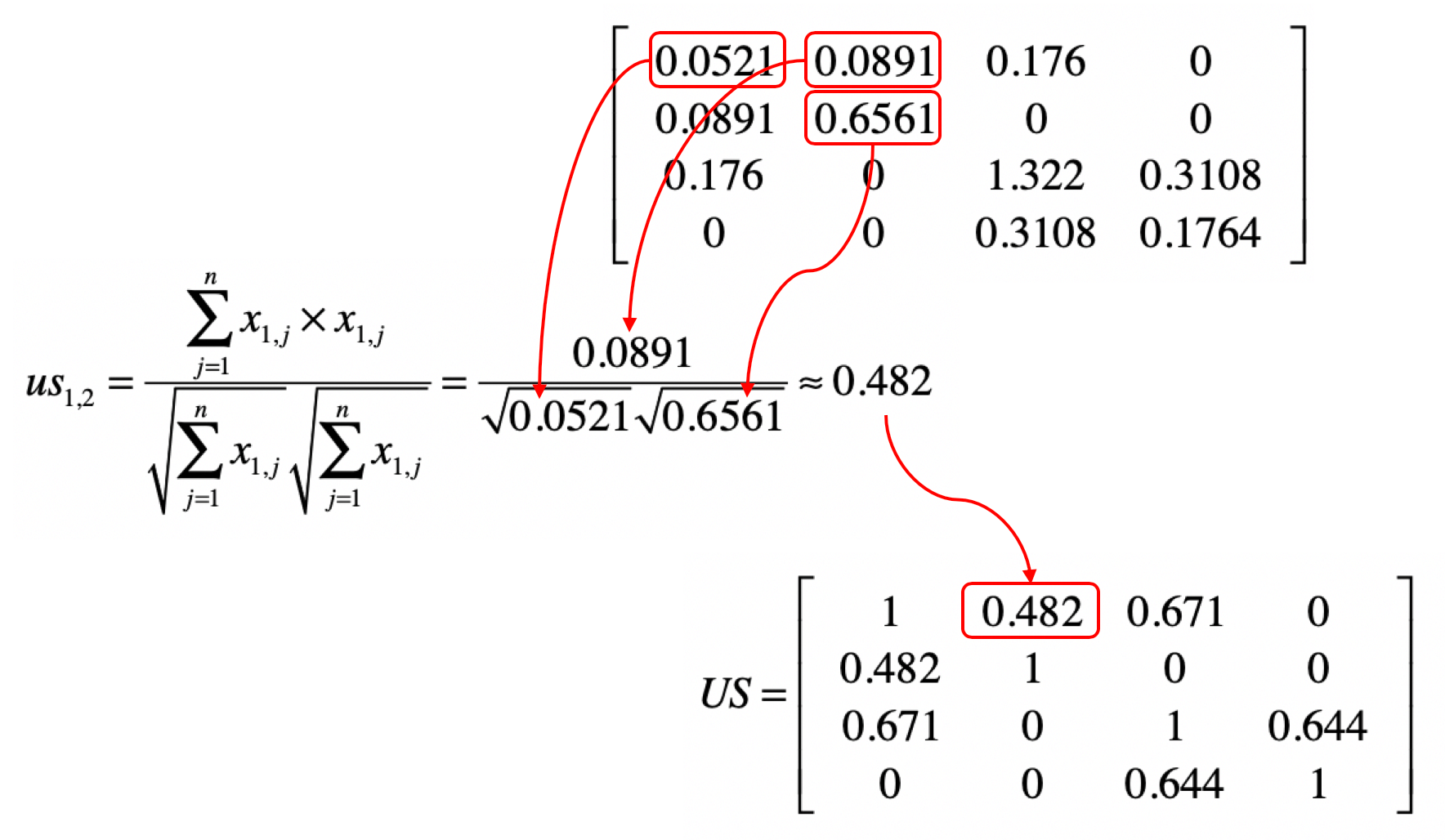
我们假设 的结果为矩阵 ，那么 就表示用户 和用户 这两者喜好度向量的点乘结果，它就是夹角余弦公式中的分子。如果 等于 ，那么这个计算值也是夹角余弦公式分母的一部分。从矩阵的角度来看， 中任何一个元素都可能用于夹角余弦公式的分子，而对角线上的值会用于夹角余弦公式的分母。这里我们仍然使用之前的喜好度矩阵示例，来计算矩阵 和矩阵 。

首先我们来看 的计算。

然后我们使用 来计算 。我用下面这张图表示矩阵中的元素和夹角余弦计算的对应关系。

明白了上面这个对应关系，我们就可以利用矩阵 ，获得任意两个用户之间的相似度，并得到一个 m×m 维的相似度矩阵 。矩阵 中 的取值为第 个用户与第 个用户的相似度。这个矩阵是一个沿对角线对称的矩阵。根据夹角余弦的定义， 和 是相等的。通过示例的矩阵 ，我们可以计算矩阵 。我把相应的结果列在了下方。

接下来，我们再来看第二个公式。

从矩阵的角度来看，现在我们已经得到用户相似度矩阵 ，再加上用户对物品的喜好度矩阵 ，现在需要计算任意用户对任意物品的喜好度推荐矩阵 。

为了实现上面这个公式的分子部分，我们可以使用 和 的点乘。我们假设点乘后的结果矩阵为 。这里我列出了根据示例计算得到的矩阵 。

分母部分可以使用 矩阵的按行求和来实现。我们假设按行求和的矩阵为 。根据示例计算就可以得到 。

最终，我们使用 和 * 的元素对应除法，就可以求得矩阵 。

既然已经有 这个喜好度矩阵了，为什么还要计算 这个喜好度矩阵呢？实际上， 是已知的、有限的喜好度。例如用户已经看过的、购买过的、或评过分的物品。而 是我们使用推荐算法预测出来的喜好度。

即使一个用户对某个物品从未看过、买过、或评过分，我们依然可以通过矩阵 ，知道这位用户对这个物品大致的喜好程度，从而根据这个预估的分数进行物品的推荐，这也是协同过滤的基本思想。从根据示例计算的结果也可以看出这点，在原始矩阵 中第 1 个用户对第 3 个物品的喜好度为 0。可是在最终的喜好度推荐矩阵 P 中，第 1 个用户对第 3 个物品的喜好度为 0.278，已经明显大于 0 了，因此我们就可以把物品 3 推荐给用户 1。

上面这种基于用户的协同过滤有个问题，那就是没有考虑到用户的喜好程度是不是具有可比性。假设用户的喜好是根据对商品的评分来决定的，有些用户比较宽容，给所有的商品都打了很高的分，而有些用户比较严苛，给所有商品的打分都很低。分数没有可比性，这就会影响相似用户查找的效果，最终影响推荐结果。这个时候我们可以采用之前介绍的特征值变化，对于原始的喜好度矩阵，按照用户的维度对用户所有的喜好度进行归一化或者标准化处理，然后再进行基于用户的协同过滤。

基于物品的过滤

基于物品的协同过滤是指利用物品相似度，而不是用户间的相似度来计算预测值。我同样用图来帮助你理解。

在这张图中，物品 A 和 C 因为都被用户 A 和 B 同时访问，因此它们被认为相似度更高。当用户 C 访问过物品 A 后，系统会更多地向用户推荐物品 C，而不是其他物品。

基于用户的协同过滤同样有两个公式，你可以看一下。

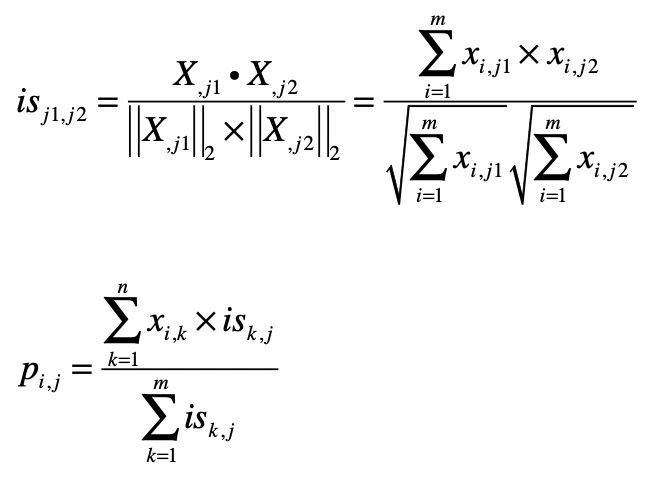
如果你弄明白了基于用户的过滤，那么这两个公式也就不难理解了。第一个公式的核心思想是计算物品和物品之间的相似度，在这里我仍然使用夹角余弦。其中 , 表示物品 和 的相似度，而 表示了 中第 列的列向量，而 表示了 中第 列的列向量。分子是两个表示物品的列向量之点乘，而分母是这两个列向量 范数的乘积。

第二个公式利用第一个公式所计算的物品间相似度，和用户对物品的喜好度，预测任一个用户对任一个物品的喜好度。其中 表示第 用户对第 个物品的喜好度， 表示用户 对物品 的喜好度， 表示物品 和 之间的相似度，注意这里除以 是为了进行归一化。从这个公式可以看出，如果 越大， 对最终 的影响越大，反之如果 越小， 对最终 的影响越小，充分体现了“基于相似物品”的推荐。

类似地，用户喜好程度的不一致性，同样会影响相似物品查找的效果，并最终影响推荐结果。我们也需要对于原始的喜好度矩阵，按照用户的维度对用户的所有喜好度，进行归一化或者标准化处理。

总结

今天我首先简要地介绍了推荐系统的概念和主要思想。为了给用户提供可靠的结果，推荐系统需要充分挖掘历史数据中，用户和物品之间的关系。协同过滤的推荐算法就很好地体现了这一点。

一旦涉及用户和物品的这种二元关系，矩阵就有用武之地了。我通过矩阵来表示用户和物品的关系，并通过矩阵计算来获得协同过滤的结果。协同过滤分为基于用户的过滤和基于物品的过滤两种，它们的核心思想都是相同的，因此矩阵操作也是类似的。在这两个应用场景下，矩阵点乘体现了多个用户或者物品之间的相似程度，以及聚集后的相似程度所导致的最终推荐结果。

当然，基于用户和物品间关系的推荐算法有很多，对矩阵的操作也远远不止点乘、按行求和、元素对应乘除法。我后面会介绍如何使用矩阵的主成分分析或奇异值分解，来进行物品的推荐。

思考题

我在介绍推荐算法时，提到了基于物品的协同过滤。请参照基于用户的协同过滤，写出相应的矩阵操作步骤。

欢迎留言和我分享，也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。