01 | 线性结构检索:从数组和链表的原理初窥检索本质

讲述:陈东
时长12:35大小8.66M
数组和链表有哪些存储特点?
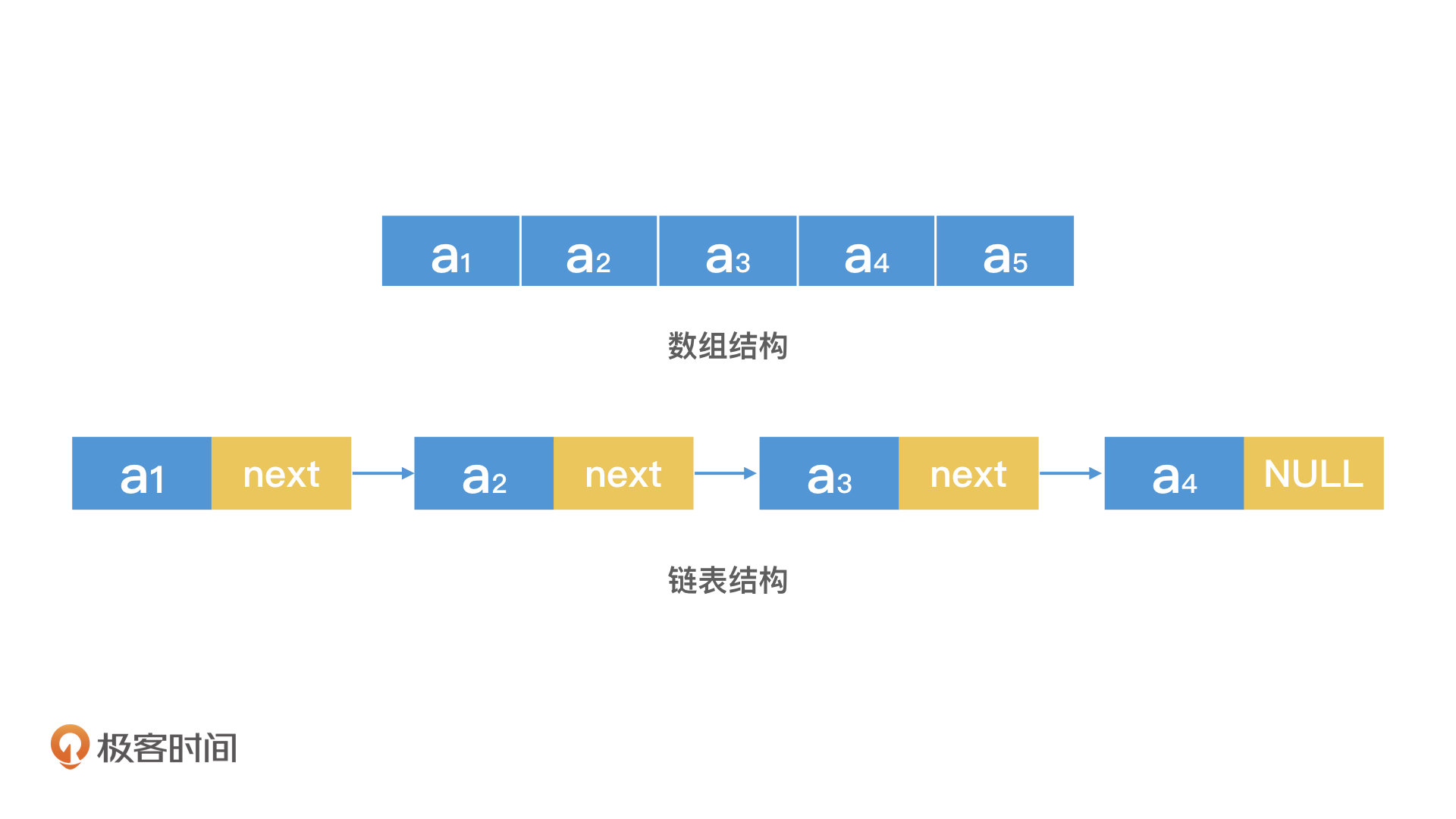
如何使用二分查找提升数组的检索效率?
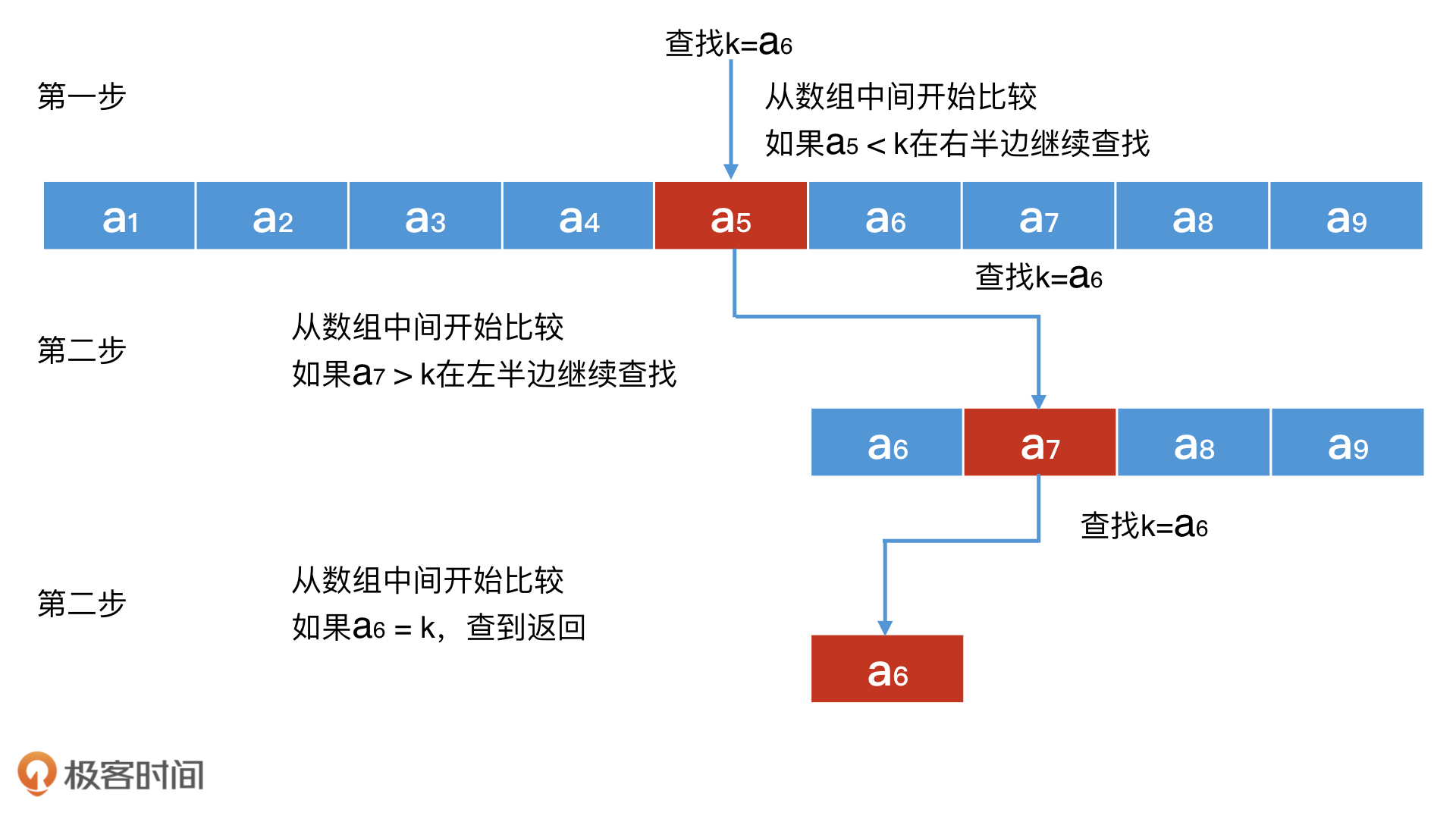
链表在检索和动态调整上的优缺点
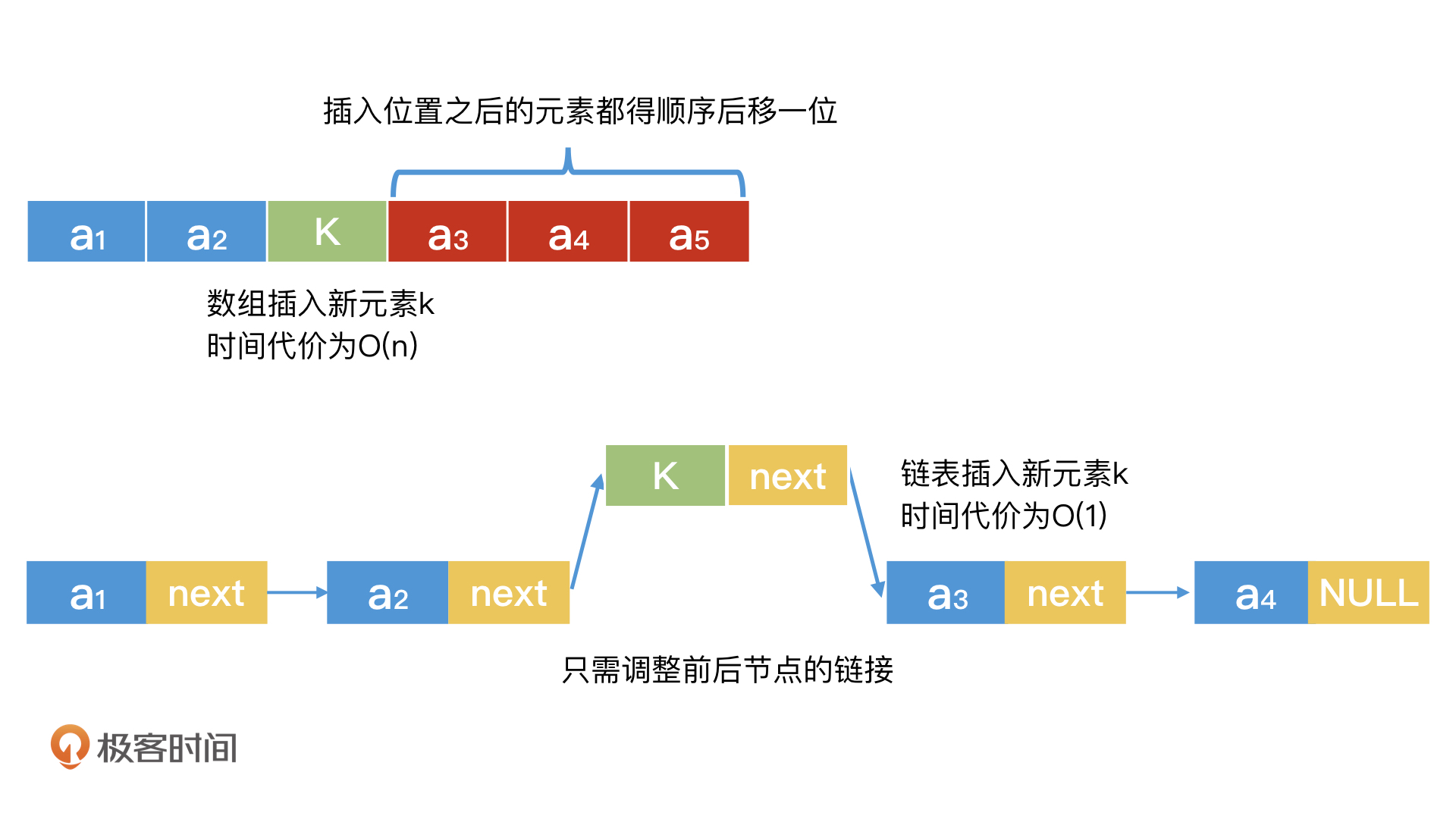
如何灵活改造链表提升检索效率?
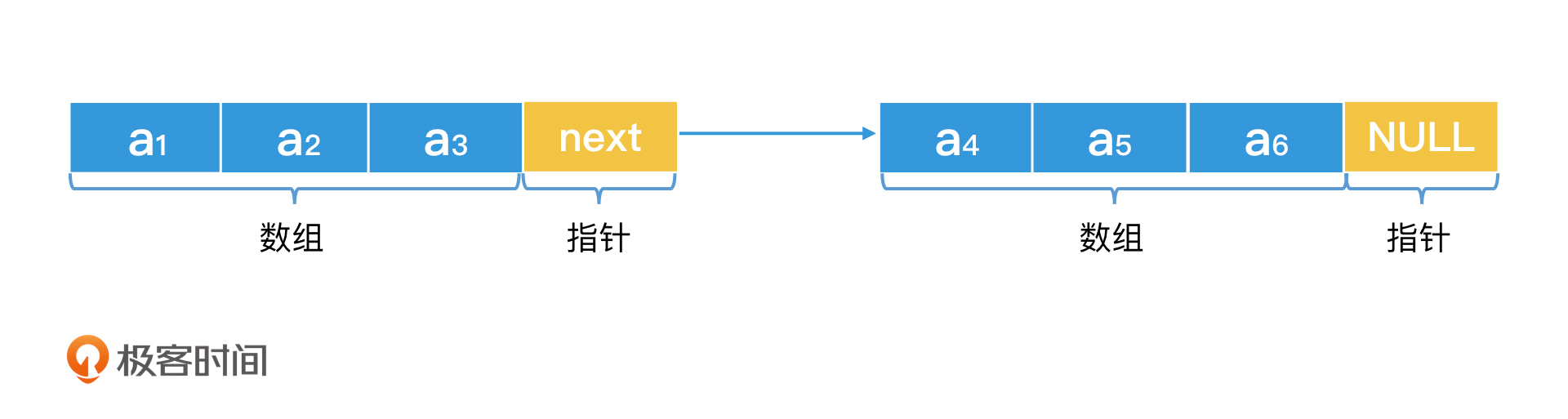
重点回顾
课堂讨论

1716143 665 拼课微信(8)
- 2020-03-23按概率算,二分肯定所需信息量最小阿,log1/2+log1/2小于log0.4+log0.6
作者回复: 用信息论的知识来分析很棒!不过如果是46分的话,出现在6那边的概率是高的,信息量就变小了。可以类比抛硬币,如果硬币出现一面的概率很高,甚至总是出现正面,那么抛硬币的信息量就很小甚至为0。
不过,对于不熟悉信息论的小伙伴也不用担心,该专栏所有的内容都会以直观能理解的语言进行讲解。不会使用大量公式或理论,做到深入浅出,可以放心学习。 2 - 2020-03-23第一个问题,二分查找概率更加均匀,没有偏向任何一端,性能波动小,速度平稳。第二个问题一次性先用二分先找到x再二分找到y,中间的都是区间内的元素展开
作者回复: 没错!很清晰👍
1 2 - 2020-03-241.二分查找概率均匀
2.分别用二分查找 x 和 y 对应的下标,然后取中间的数据展开作者回复: 简明扼要👍
1 - 2020-03-24问题1:难道是和太极的“阴阳”有关?所以一分为二。
问题2:
1. 二分法查找出x、y;
2. x与y之间的所有元素就是的x到y索引的区间[x索引, y索引]包含的数据。展开作者回复: “太极生两仪,两仪生四象,四象生八卦”。你会发现,这就是一个不断二分的过程。可见,二分的思想在许多地方都有体现。
二分的好处是平衡。不会出现最差情况。如果是3-7分,那如果总是要在多数元素的这一半进行查找,那么查找次数就会变多。 1 1 - 2020-03-23对于第二题,有点疑惑想问下老师,对于正常的情况(x<=y),我想到的可以有两种方法去实现,第一种方法是先二分查找x,然后二分查找y,x和y之间的元素就是答案了。第二种方法就是只二分查找x或者y,然后去顺序遍历,和另一个去比较。但是我觉得这两种方法对于不同x和y效率应该是不一样的,有些情况第一种方法较快,有些情况第二种方法较快,想问下老师工业界中的产品(redis)是如何实现区间查询的呢?展开
编辑回复: 非常好!你很好地实践了导读中的学习方法:“多问为什么,多对比不同的方法寻找优缺点”。
1.对于数组怎么范围的问题:
对x和y分别做两次二分查找,时间代价为log(n)+log(n)。
而对x做二分查找,再遍历到y,时间代价为log(n)+(y-x)。
发现没有,我们完全可以根据log(n)和(y-x)的大小进行预判,哪个更快就选哪个!
当然,除非y-x非常小,否则一般情况下log(n)会更小。
2.对于Redis是怎么实现的问题:
在下一课中,你会学习到,Redis是使用跳表实现的。而跳表是“非连续存储空间”。因此,它不能像数组一样,直接将x到y之间的元素快速复制出来到结果集合中,因此,它只能通过遍历的方式将范围查找的结果写入结果集合中。 2 1 - 2020-03-23个人觉得二分更方便,三七分和四六分都会让一边大一边小越来越难分
对有序数组,先查询最小值的索引,在查询最大值的索引,两者之间的所有值就是这个区间的所有元素展开作者回复: 二分的确更方便,但不仅仅是代码方便,而是它更加平衡,整体性能稳定,能避免出现最坏情况,否则如果是一直在大的一边查找,那么查找次数就会变多
1 - 2020-03-23第一个思考题是不是二分更容易计算编写代码
第二个思考题 先找第一个大于x 然后在找最后一个小于y 这样子就确定了区间。展开作者回复: 二分不不仅仅是容易写代码,更重要的是能均匀划分查询空间。避免出现最坏情况。否则如果一边大一边小,那么最坏情况下,会一直在大的一边进行查找,使得查找次数变多。
1 - 2020-03-24高手很多啊展开