04 | 状态检索:如何快速判断一个用户是否存在?

讲述:陈东
时长15:56大小14.61M
如何使用数组的随机访问特性提高查询效率?
如何使用位图来减少存储空间?
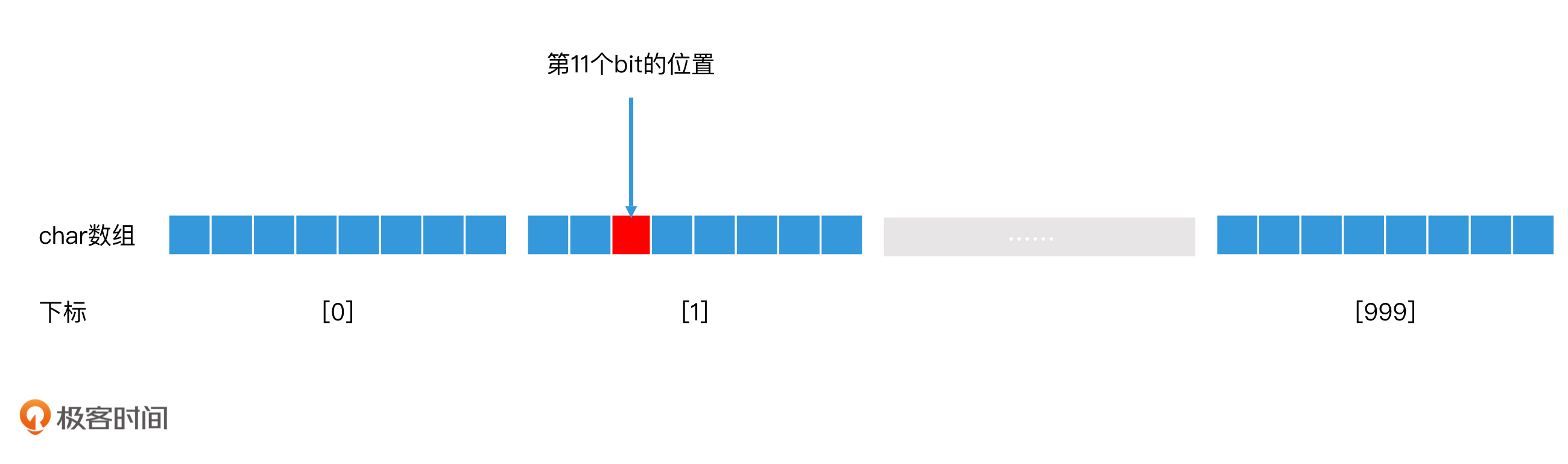
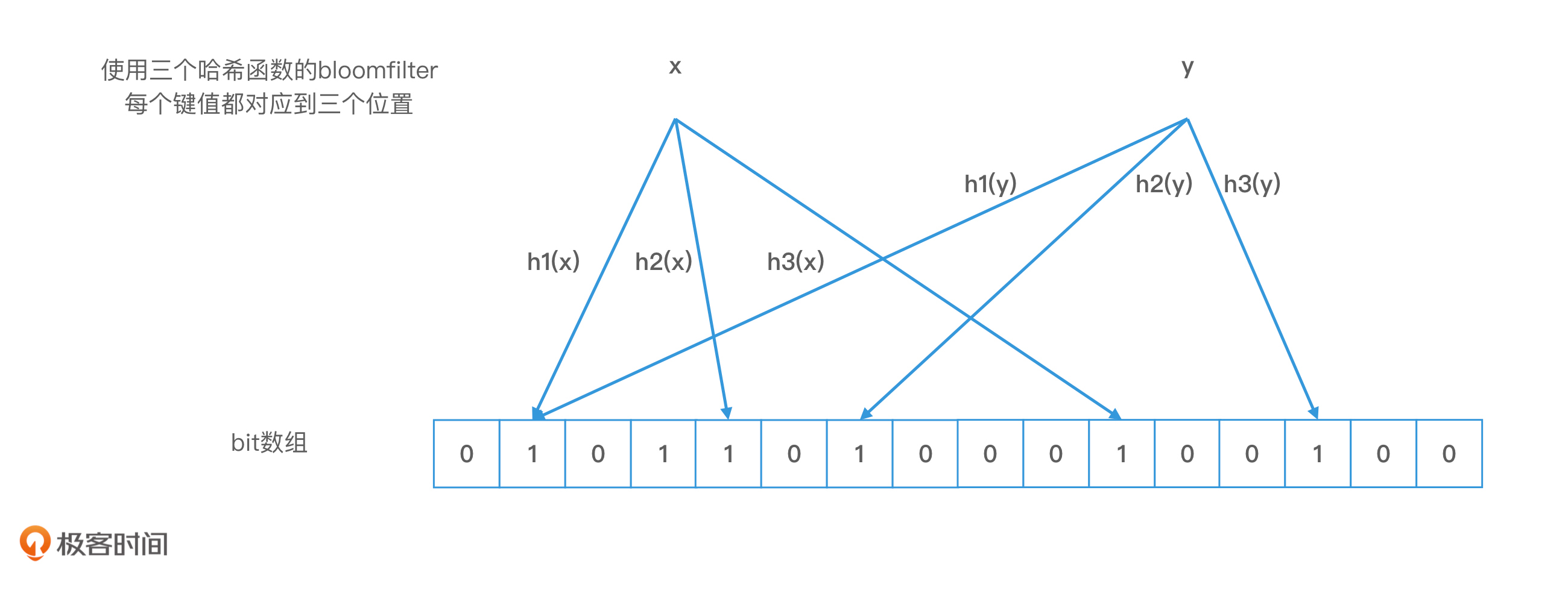
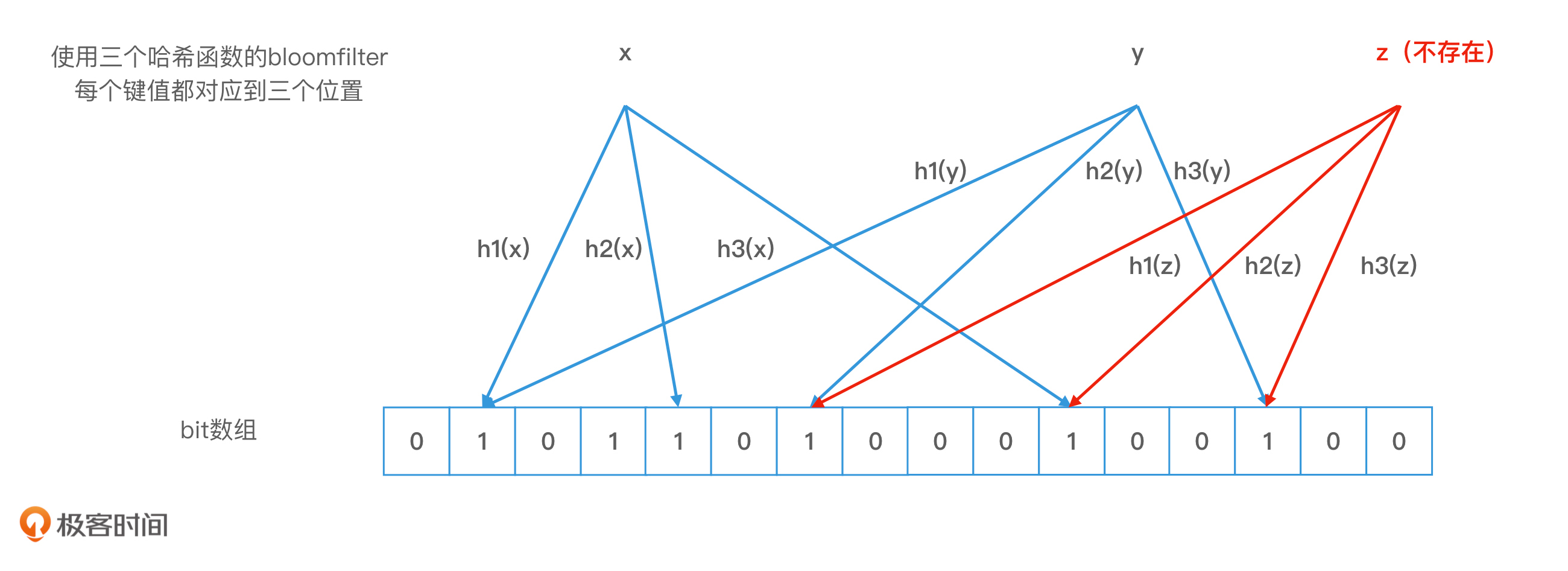
重点回顾
课堂讨论

171614 3665 拼课微信(7)
- 2020-03-30因为同一个ID经过哈希函数会得到多个位置,不同的ID可能会有一些位置overlap。如果ID A和B刚好有一个位置重合,那么删除A的时候,如果直接将它对应的位置清零,就导致B也被认为是不存在。因此bloom filter删除操作很麻烦展开
作者回复: 是的。bloom filter的删除会很麻烦。我们一般用在数据不删除的场景中(比如文中举的注册ID的场景)。
如果真要删除,可以使用上一课提到的re-hash的思路重新生成。(因为bloom filter本来就允许错误率,因此可以周期性重新生成)。
此外,还可以将bloomfilter改造成带引用计数的。 1 2 - 2020-03-30bitmap 是一个集合,每个元素在集合中有一个唯一不冲突的编号(用户自己保证,在数据库中这个编号可以是行号),是双射关系。而布隆过滤器是一个不准确的集合,而且是一对多的关系,会发生冲突,也就是说布隆过滤器的为1的位可能代表多个元素,自然不能因为一个元素删除就把它干掉?,或者说他就不支持删除操作,感觉它要支持了,反而把它本身的优势给丢了。
1,其实对布隆过滤器是省了空间,我表示持怀疑态度,可能需要证明下,我可能更多的认为它是一种平衡单个hash 函数对数据分布有偏差性导致最差情况的数据冲突的概率大的一种方法。
2,bitmap 本身也有很多压缩方法,最有名的应该是roaringbitmap ,大家有兴趣可以了解下。展开作者回复: 你的思考很深入!
1.对于布隆过滤器的删除问题,的确无法直接删除。但也有带引用计数的布隆过滤器,存的不是0,1,而是一个计数。其实所有的设计都是trade off。应该视具体使用场景而定。比如一个带4个bit位计数器的布隆过滤器,相比于哈希表依然有优势。
2.布隆过滤器是否省空间,要看怎么比较。
布隆过滤器 vs 原始位图:
原始位图要存一个int 32的数,就要先准备好512m的空间的长数组。布隆过滤器不用这么长的数组,因此比原始位图省空间。
布隆过滤器 vs 哈希表:
假设布隆过滤器数组长度和哈希表一样。但是哈希表存的是一个int 32,而布隆过滤器存的是一个bit,因此比同样长度的哈希表省空间。
当然,如果哈希表也改为只存一个bit的数组,那么他们的大小是一样的。这时候就是你说的多个哈希函数的作用场景了。
其实,你会发现,只存一个bit的哈希表,其实也可以看做是只有一个哈希函数的布隆过滤器。很多时候,布隆过滤器,哈希表,还有位图,它们的边界是模糊的。我们最重要的是了解清楚他们的特点,知道在什么场景用哪种结构就好了。
3.roaring bitmap是一个优秀的设计。我在基础篇的加餐中会和大家分享。在这里,我也说一下它和布隆过滤器的差异:
布隆过滤器 vs roaring bitmap:
所有的设计都是trade off。roaring bitmap尽管压缩率很高,还支持精准查找,但是它放弃的是速度。高16位是采用二分查找,array container也是二分查找。因此,在这一点上布隆过滤器是有优势的。此外,它还不能保证压缩空间,它的空间会随着元素增多而变大,极端情况下恢复回bitmap。
而布隆过滤器保持了高效的查找能力和空间控制能力,但是放弃了精准查找能力,精准度会随着元素增多而下降。
因此,尽管都是对bitmap进行压缩,但是两者的设计思路不一样,使用场景也不同。在不要求精准,但是要求快速和省空间的场景下,布隆过滤器是不错的选择。 2 - 2020-03-30增加可以容忍误判,错误的判断用户存在,换个账号注册就行了,那么删除也会存在误判,可能将真正的用户没有删除掉,这可就不可取了,老师,我蒙对没,算法好头疼
作者回复: 你可以看我文中的例子想一想,x和y有共同的位,因此,如果删除x时,把x对应的3个bit位都改为0,就会影响y的查询。因此,对于布隆过滤器,不能直接删除。
一般来说,我们可以周期性重建布隆过滤器解决这个问题。
算法是不容易。但是不着急,慢慢来,一步一步扎扎实实学,你会收获得更多。 - 2020-03-30位图 一个位置就只有一个元素使用,布隆过滤器一个位置可能多个元素都会使用
作者回复: 是的。所以布隆过滤器不能直接删除。如果真的发生了删除,可以用类似re-hash的机制重新生成。
此外,一些场景会将布隆过滤器改造为带引用计数的结构。通过一个小数值的count进行计数。 - 2020-03-30会造成其他元素存在状态的错误判断,因为多个对象可能共用一个元素。但是极端情况下,甚至有可能一个对象对应的K个元素都与其他对象共用,这种情况下不知道该怎么办了,请老师帮忙解答一下,谢谢
作者回复: 的确,一般来说布隆过滤器是不能直接删除的。它适用于数据不删除的场景(比如文中举的注册id的场景)。如果真有删除需求,可以像前一课学过的re-hash一样,重新生成。
此外,删除频繁的场景下,还可以将布隆过滤器带上计数器。就是将一个bit改为4个bit,可以存一个数。
尽管空间变大了,但是依然比哈希表存一个int 32的元素更省空间。 - 2020-03-30对于布隆过滤器,删除元素时如果将对应的k个元素全部设置为0的话,会影响其他元素的判断,我想到一个方法,就是对于每一个数组中每一位,再设置一个标志count,用于记录出现1得次数,删除元素时将count减1,如果count为0的话,再将1设置为0。但是这样做的话,存储count不是又需要花费存储空间,这与布隆过滤器的设计目的不就冲突了吗?想知道布隆过滤器对于删除元素时如何实现的?希望老师解答。展开
作者回复: 布隆过滤器的确是无法直接删除的。要删除的话,有两种思路,一种就是重新生成(和re-hash一个思路)。另一种就是你说的引用计数。
其实引用计数是可行的。它的确性能会比原始的布隆过滤器差,但依然好于哈希表。因为我们对于引用计数,完全可以用少数几个bit位来记录,比如说4个比特位就能记录到16。
这样的存一个4bit计数值的布隆过滤器,依然会比存int 32的哈希表更省空间。
所有的设计都是要根据具体场景灵活变通。因此,如果应用场景真的有频繁删除的需求,那么这样一种结构也是可以考虑的。 1 - 2020-03-301.bitmap和bloomfilter都是为了判断状态存在的。
2.bitmap只有一个位置用来判断状态
3.bloomfilter有多个位置用来判断状态
4.针对bloomfilter来说若果不所在一定不存在,存在不一定存在(因为hash冲突,可能是另外的元素状态)
5.如何根据用户数量来确定bitmap或者bloomfilter的bit数组的大小呢?展开作者回复: 总结得很好!
对于第五个问题,如何确定大小:
如果是原始位图,假设id是int 32,如果你不清楚数值分布范围,那么只能覆盖所有int 32的取值区间。这时候的位图大小是512m。
如果是布隆过滤器,你需要预估你的用户数量,
此外,还要设置一个你能接受的错误率p,使用这个公式:m =-n ln p / (ln 2)^2 ,可以算出来bit 位数组m的大小。