14 | 空间检索（下）：“查找最近的加油站”和“查找附近的人”有何不同？

2020-04-27 陈东

检索技术核心20讲

进入课程



讲述：陈东

时长17:00大小15.57M



你好，我是陈东。
上一讲我们讲了，对于查询范围固定的应用需求，比如“查找附近的人”，我们可以根据规划好的查询区域大小，均匀划分所有的空间，然后用 GeoHash 将坐标转换为区域编码，以该区域编码作为 Key 开始检索。这样，我们就可以查到并取出该区域中的目标数据，对这些数据进行精准计算然后排序输出了。
但是，并不是所有应用的查询范围都是不变的。在一些基于地理位置的服务中，我们并不关心检索结果是否就在我们“附近”，而是必须要找到“最近”的一批满足我们要求的结果。这怎么理解呢？
我来举个例子，我们在长途自驾游的时候，突然发现车快没油了。这个时候，我们要在一个导航地图中查找最近的 k 个加油站给车加油，这些加油站可能并不在我们附近，但地图又必须要返回最近的 k 个结果。类似的情况还有很多，比如说，我们要查询最近的医院有哪些，查询最近的超市有哪些。那对于这一类的查询，如果当前范围内查不到，系统就需要自动调整查询范围，直到能返回 k 个结果为止。
对于这种需要动态调整范围的查询场景，我们有什么高效的检索方案呢？今天，我们就来探讨一下这个问题。
直接进行多次查询会有什么问题？我们就以查找最近的加油站为例，一个直观的想法是，我们可以先获得当前位置的 GeoHash 编码，然后根据需求不停扩大查询范围进行多次查询，最后合并查询结果。这么说比较抽象，我们来分析一个具体的位置编码。
假设我们当前地址的 GeoHash 编码为 wx4g6yc8，那我们可以先用 wx4g6yc8 去查找当前区域的加油站。如果查询的结果为空，我们就扩大范围。扩大查询范围的思路有两种。
第一种思路是，一圈一圈扩大范围。具体来说就是，我们第一次查询周边 8 个邻接区域，如果查询结果依然为空，就再扩大一圈，查询再外圈的 16 个区域。如果还是不够，下一次我们就查询再外圈的 24 个区域，依此类推。你会发现，这种方案的查询次数会成倍地增加，它的效率并不高。
逐步扩大查询周边区域
另一种思路是，我们每次都将查询单位大幅提高。比如说，直接将 GeoHash 编码去掉最后一位，用 wx4g6yc 再次去查询。如果有结果返回，但是不满足要返回 Top K 个的要求，那我们就继续扩大范围，再去掉一个编码，用 wx4g6y 去查询。就这样不停扩大单位的进行反复查询，直到结果大于 k 个为止。
逐步扩大查询单位
和第一种查询思路相比，在第二种思路中，我们每次查询的区域单位都得到了大范围的提升，因此，查询次数不会太多。比如说，对于一个长度为 8 的 GeoHash 编码，我们最多只需要查询 8 次（如果要求精准检索，那每次查询就扩展到周围 8 个同样大小的邻接区域即可，后面我就不再解释了）。
这个检索方案虽然用很少的次数就能“查询最近的 k 个结果”，但我们还需要保证，每次的查询请求都能快速返回结果。这就要求我们采用合适的索引技术，来处理 GeoHash 的每个层级。
比如说，如果使用基于哈希表的倒排检索来实现，我们就需要在 GeoHash 每个粒度层级上都分别建立一个单独的倒排表。这就意味着，每个层级的倒排表中都会出现全部的加油站，数据会被复制多次，这会带来非常大的存储开销。那我们是否有优化存储的方案呢？
我们可以利用 GeoHash 编码一维可排序的特点，使用数组或二叉检索树来存储和检索。由于数组和二叉检索树都可以支持范围查询，因此我们只需要建立一份粒度最细的索引就可以了。这样，当我们要检索更大范围的区域时，可以直接将原来的查询改写为范围查询。具体怎么做呢？
我来举个例子。在检索完 wx4g6yc8 这个区域编码以后，如果结果数量不够，还要检索 wx4g6yc 这个更大范围的区域编码，我们只要将查询改写为“查找区域编码在 wx4g6yc0 至 wx4g6ycz 之间的元素”，就可以利用同一个索引，来完成更高一个层级的区域查询了。同理，如果结果数量依然不够，那下一步我们就查询“区域编码在 wx4g6y00 至 wx4g6yzz 之间的元素”，依此类推。
利用有序数组查询示例
但是，这种方案有一个缺点，那就是在每次调整范围查询时，我们都要从头开始进行二分查找，不能充分利用上一次已经查询到的位置信息，这会带来无谓的重复检索的开销。那该如何优化呢？你可以先想一想，然后我们一起来看解决方案。
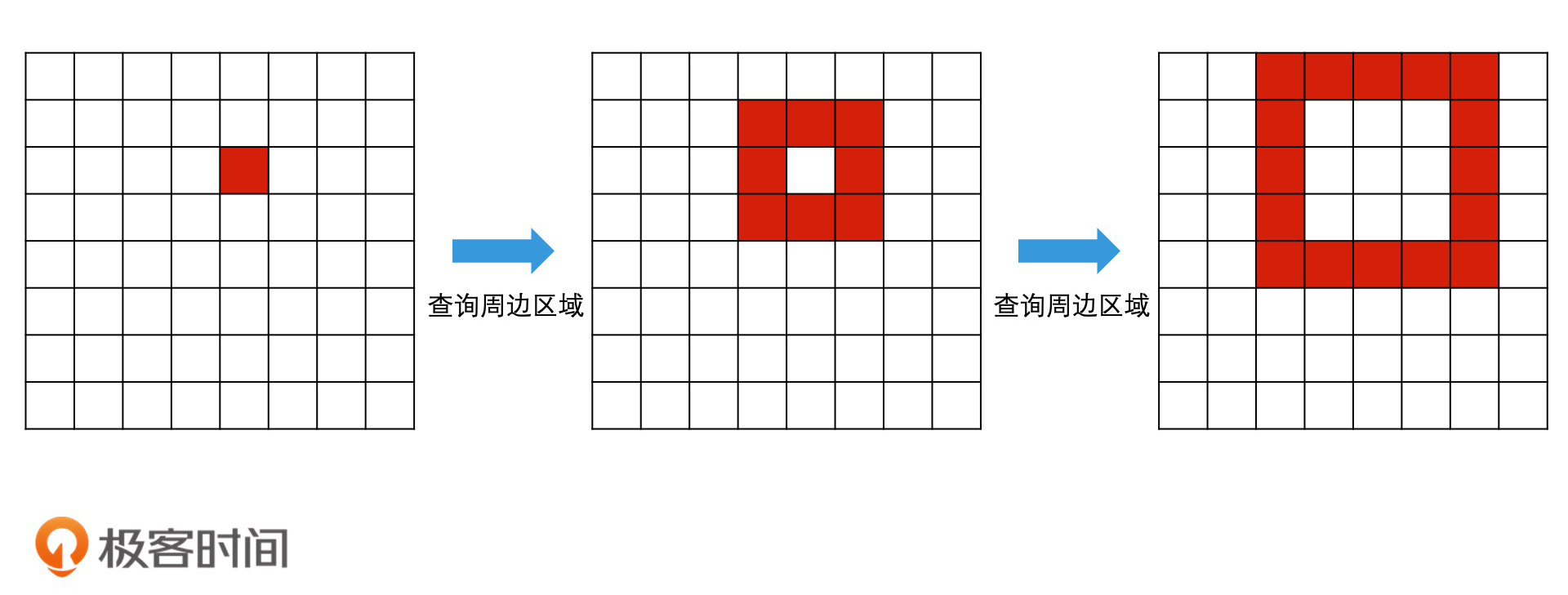
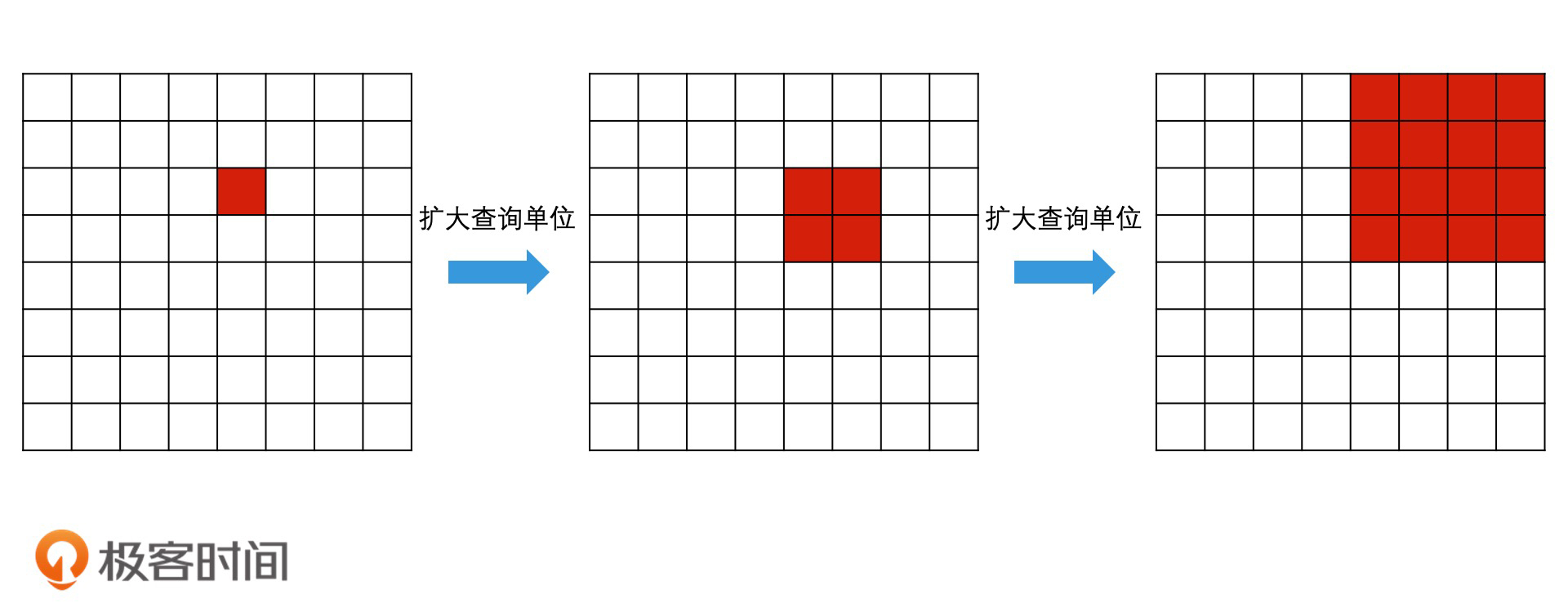
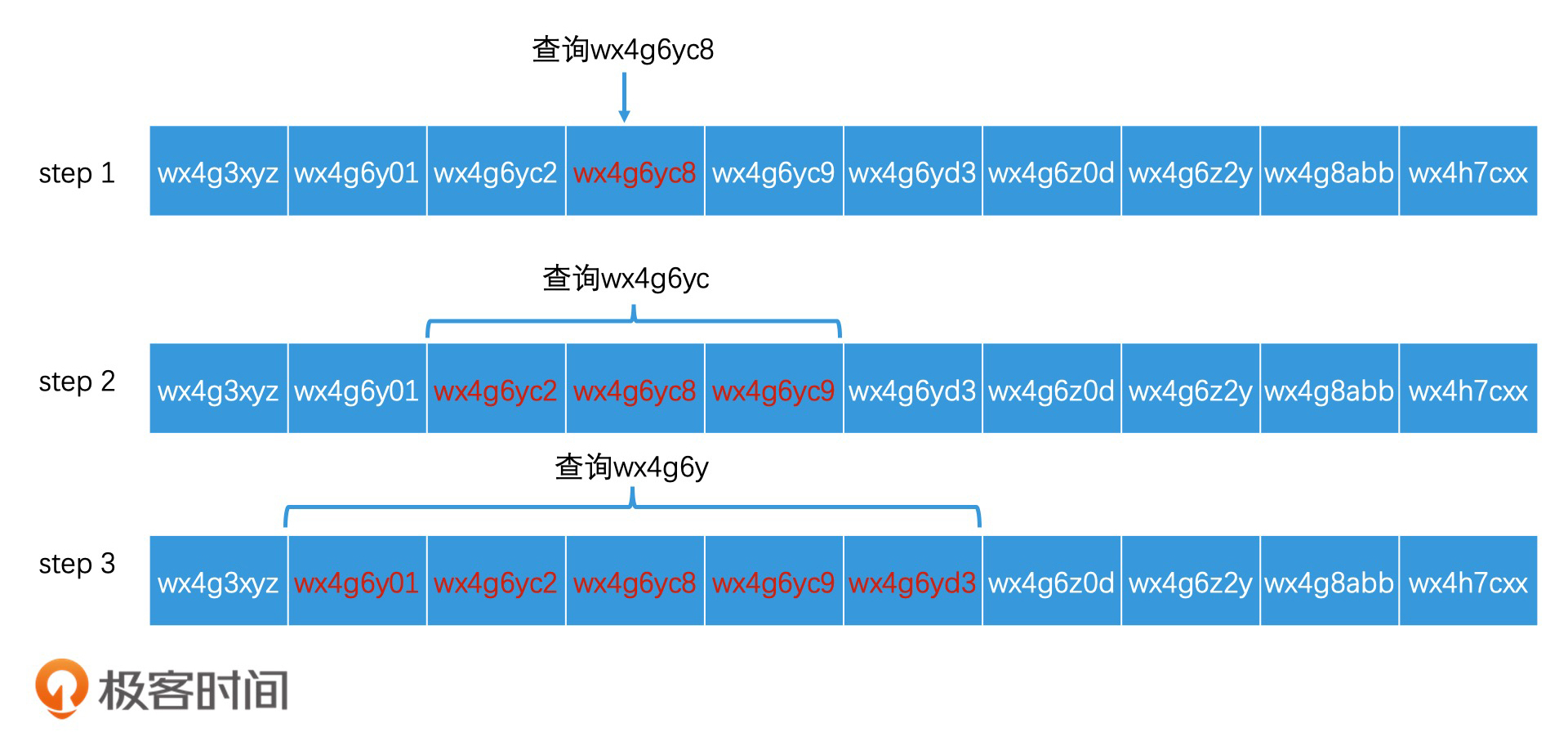
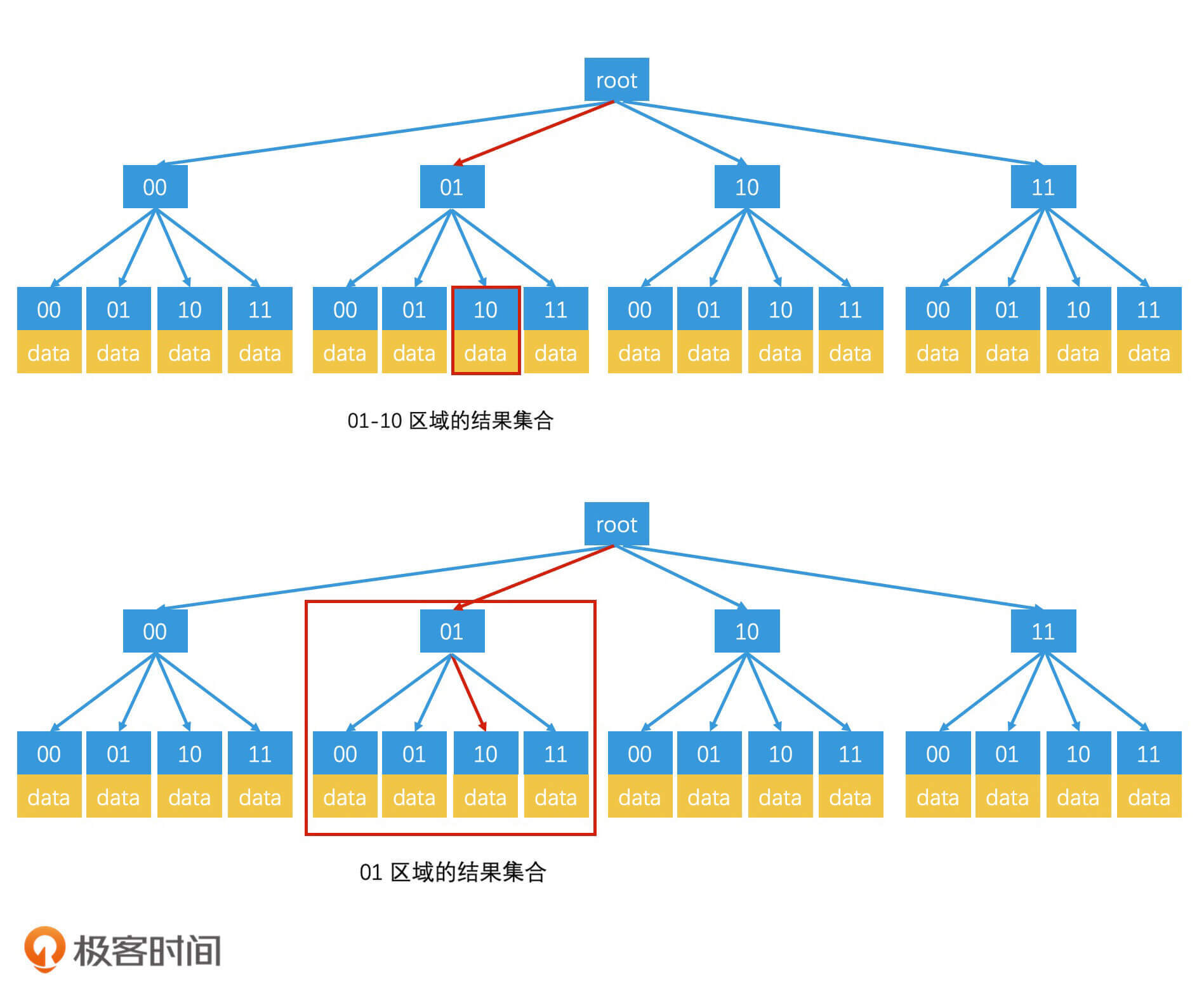
如何利用四叉树动态调整查询范围？上一讲我们讲过，许多系统对于 GeoHash 的底层实现，其实都是使用二进制进行存储和计算的。而二进制区域编码的生成过程，就是一个逐渐二分空间的过程，经过二分后的区域之间是有层次关系的。如果我们把这个过程画下来，它就很像我们之前讲过的树形结构。
因此，我们可以尝试用树形结构来进行索引。这里，我们就要引入一个新的数据结构四叉树了。四叉树的树根节点代表了整个空间，每个节点的四个分叉分别表示四个子空间。其中，树根和中间节点不存储数据，只记录分叉指针。而数据只记录在最小的区域，也就是叶子节点上。
如果我们从根节点开始，不停地四分下去，直到每个分支的叶子节点都是最小粒度区域。那这样构建出来的四叉树，每个节点都有四个子节点，就叫作满四叉树。
对于满四叉树的每个节点，我们都可以编号。换句话说，我们可以按 00、01、10、11 的编号，来区分满四叉树的四个子节点。这样一来，只要我们从根节点遍历到叶子节点，然后将路径上每个节点的编号连起来，那最后得到的编码就是这个叶子节点所代表的区域编码。
满四叉树
好了，现在我们知道了四叉树的结构和特点了，那我们怎么利用它完成自动调整范围的 Top K 检索呢？下面，我们通过一个例子来看看。
假设一个人所属的最小区域编码是 0110，那我们在检索的时候，就以 0110 为 Key，沿着四叉树的对应分支去寻找相应的区域，查询路径为 01-10。如果查找到了叶子节点，并且返回的结果大于 k 个，就可以直接结束检索。如果返回结果不足 k 个，我们就得递归返回到上一层的父节点，然后以这整个父节点的区域编码为目标进行检索。这样，我们就避免了要再次从树根检索到父节点的开销，从而提升了检索效率。
自动调整范围的Top K检索
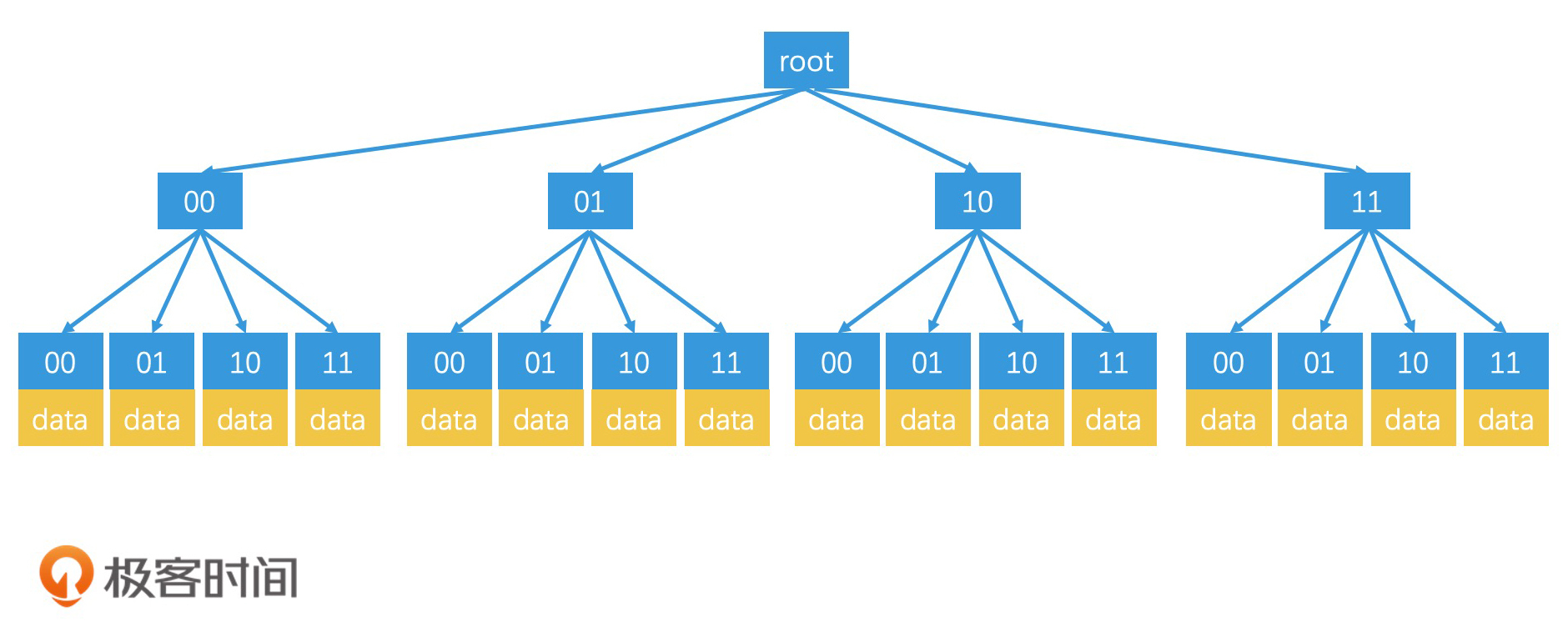
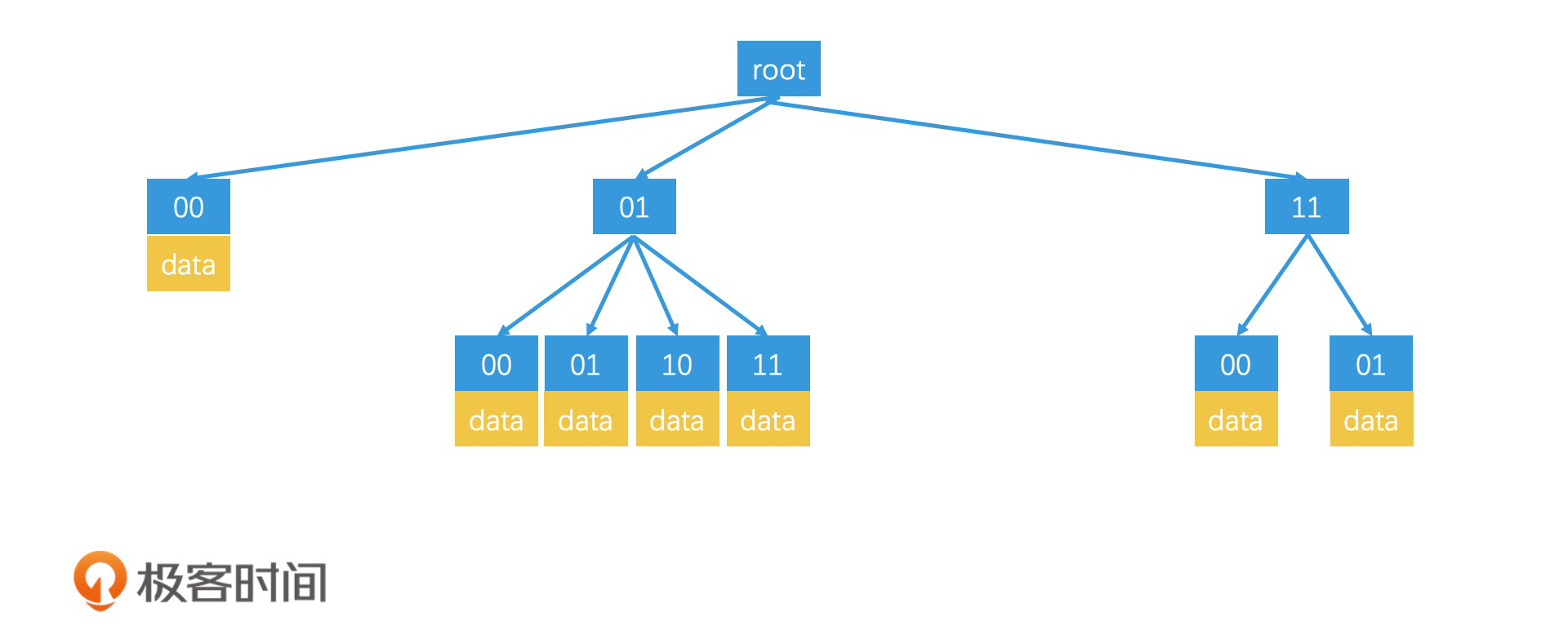
如何利用非满四叉树优化存储空间？尽管，我们使用以最小区域单位为叶子节点的满四叉树，能够很好的提升检索效率，但是在数据稀疏的时候，许多叶子节点中的数据可能是空的，这就很有可能造成大量的空间浪费。为了避免出现空间浪费，我们有一种改进方案是，使用动态节点分裂的非满四叉树。
首先，我们可以给每个叶子节点规定一个容纳上限。比如说，我们可以将上限设置为 n。那么，一开始的四叉树只有一个根节点，这个根节点同时也是叶子节点，它表明了当前的全部空间范围。当有数据加入的时候，我们直接记录在这个节点中，查询时也只查询这个节点即可。因此，当插入的数据个数小于 n 时，我们不需要进行任何复杂的查找操作，只需要将根节点的所有数据读出，然后进行距离计算并排序即可。
随着加入的数据越来越多，如果一个叶子节点的容量超出了容纳上限，我们就将该节点进行分裂。首先，我们将该节点转为中间节点，然后，我们会为这个节点生成 1 至 4 个叶子节点（注意：不是一定要生成 4 个叶子节点），并将原来存在这个节点上的数据都转入到对应的叶子节点中。这样，我们就完成了分裂。
不过，有一种极端的情况是，这些数据都会转入到同一个下层叶子节点上。这时，我们就需要继续分裂这个叶子节点，直到每个叶子节点的容量在阈值下为止。
通过这种动态生成叶节点的方案，我们就能得到一棵非满四叉树。和满四叉树相比，它的叶子节点会更少，而且每个叶子节点表示的区域范围也可能是不一样的。这使得非满四叉树具有更好的空间利用率。非满四叉树的查询过程和满四叉树十分相似，也是根据当前的区域编码，找到对应的叶子节点，并根据该叶子节点上存储的数据数量，判断是否要递归扩大范围。这里我就不再详细说了。
非满四叉树-动态分裂叶节点
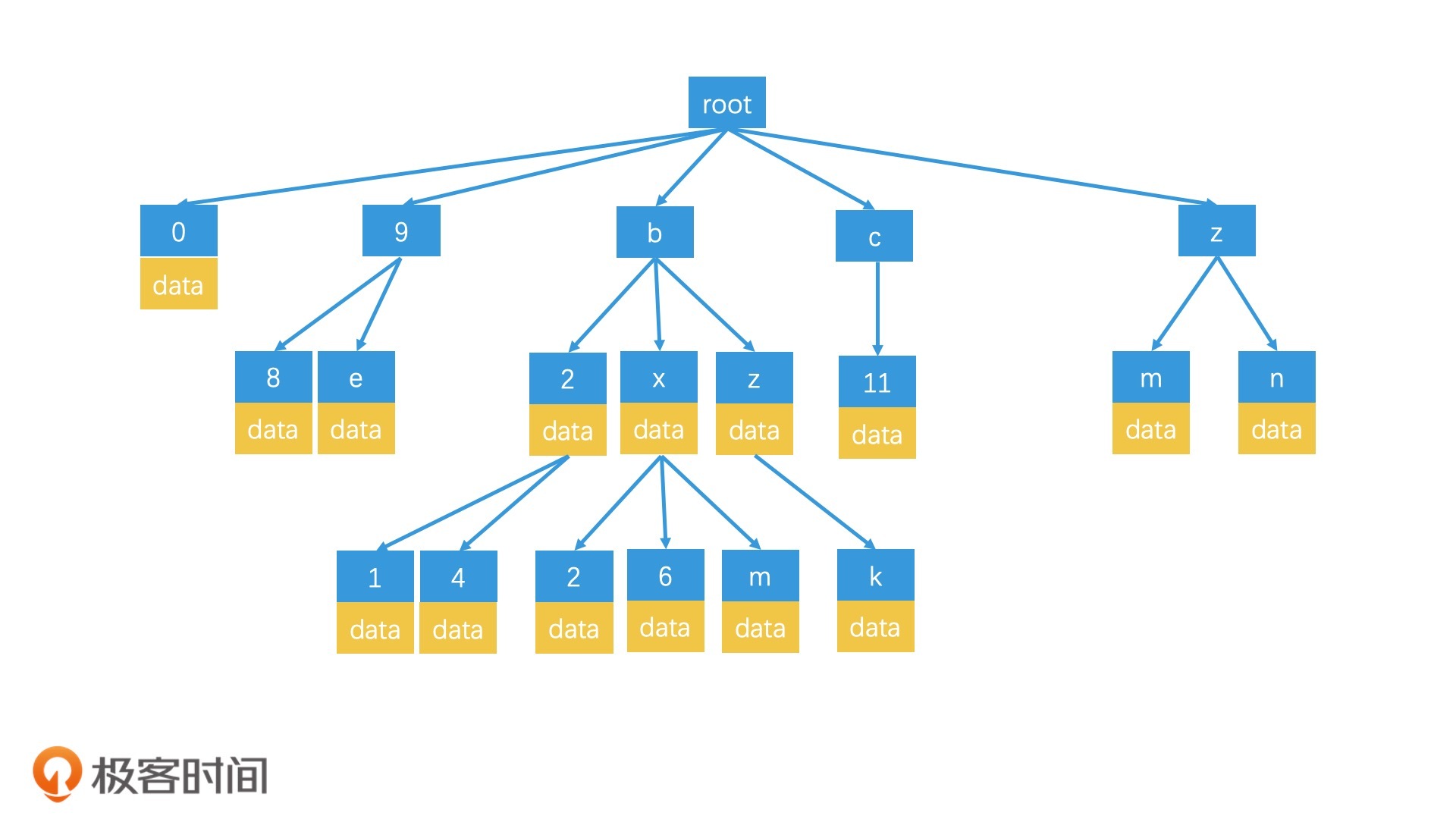
如何用前缀树优化 GeoHash 编码的索引？上面，我们都是用二进制编码来说明的。你可能会问，如果我们使用了 GeoHash 编码方式，是否也可以用类似的检索技术来索引呢？当然是可以的。实际上，对于字符串的检索，有一种专门的数据结构，叫作前缀树（Trie 树）。
前缀树的思路和四叉树非常相似，它也是一种逐层划分检索空间的数据结构。它的根节点代表了整个检索空间，然后每个中间节点和叶子节点都只存储一个字符，代表一个分支。这样，从根节点到叶子节点的路径连起来，就是一个完整的字符串。因此，当使用 GeoHash 编码来表示区域时，我们可以建立一个前缀树来进行索引，前缀树的每个节点最多会有 32 个子节点。
前缀树
那如何利用前缀树来检索呢？举个例子，当我们查询 wx4g6yc8 这个区域时，我们会沿着 w-x-4-g-6-y-c-8 的路径，检索到对应的叶子节点，然后取出这个叶子节点上存储的数据。如果这个区域的数据不足 k 个，就返回到父节点上，检索对应的区域，直到返回结果达到 k 个为止。由于整体思路和四叉树是十分相似的，这里就不展开细说了。
此外，前缀树除了用在 GeoHash 编码的检索上，也经常用于字典的检索，因此也叫字典树。字典树适用于匹配字符串的检索场合。
总结来说，利用树形结构来划分空间提高检索效率的方案，它的应用非常广泛。对于更高维度空间的最近邻检索，我们也可以使用类似的检索方案来划分空间。比如说，在三维空间中，八叉树就是常见的检索方案。那拓展到更高的维度，如 k 维，我们还可以使用 k-d 树（K-Dimensional Tree）来检索。
k-d 树一种是更通用的，对任意维度都可以使用的检索方案。k-d 树和四叉树、八叉树的检索思路并不相同，它在划分子空间的时候，并不是直接将整个空间划分为 2^k 个子空间，而是会选出最有区分度的一个维度，将该维度的空间进行二分，然后对划分出的子空间再进行同样的二分处理，所以，它实际上是一个二叉树。而且，由于它的分支数和维度 k 的具体值无关，因此具有更好的通用性。
事实上，k-d 树在维度规模不大的场景下，确实具有不错的检索效率。但是，在成百上千的超高维度的场景中，k-d 树的性能会急剧下降。那在高维空间中，我们又该如何快速地查找到最近的 k 个对象呢？这个问题，也是搜索引擎和推荐引擎在很多应用场景中都要解决问题。在后面两讲中，我们会对它作详细讲解。
重点回顾今天，我们重点学习了，在二维空间中利用四叉树，来快速寻找最近的 k 个元素的方法。
在需要动态调整查询范围的场景下，对于二进制编码的二维空间的最近邻检索问题，我们可以通过四叉树来完成。四叉树可以很好地快速划分查询空间，并通过递归的方式高效地扩大查询范围。但是满四叉树经常会造成无谓的空间浪费，为了避免这个问题，在实际应用的时候，我们会选择使用非满四叉树来存储和索引编码。对于 GeoHash 编码的二维空间最近邻检索问题，我们也能通过类似的前缀树来提高检索效率。
课堂讨论在非满四叉树的分裂过程中，为什么一个节点不一定会生成 4 个叶子节点？你能举一个例子吗？
欢迎在留言区畅所欲言，说出你的思考过程和最终答案。如果有收获，也欢迎把这一讲分享给你的朋友。

13 | 空间检索（上）：如何用Geohash实现“查找附近的人”功能？

15 | 最近邻检索（上）：如何用局部敏感哈希快速过滤相似文章？

 写留言

精选留言(7)

那时刻

2020-04-27

在GeoHash通过去掉最后一位编码的方式来扩大搜索范围，比如这次搜索了四个编码块，下次搜索16个编码块。在这16个编码块里有上次已经搜索的四个编码块，请问老师，这里应该有去重处理吧？来避免重复查询。
想到一个方式就是对于已经搜索过的hash编码标记下，避免重复搜索。

展开

作者回复: 你说的对，肯定会有去重处理。不过16个编码块是覆盖4个编码块的，因此我们直接使用16个编码块的检索结果就好了。否则对四个编码块再进行去重比较，其实代价是差不多的。

 2

 1
一步

2020-04-28

当前地址的 GeoHash 编码为 wx4g6yc8，这个根据上节学的编码规范，前4个字母代码纬度，后面四个代表经度，如果去掉最后一个字符不是代表纬度不变，经度的范围扩大 2 ^ 5 倍，这样的范围不应该是一个长方形吗？怎么会是图中的正方形呢？
----------------
作者回复: 你看得很仔细。Geohash由于是5个比特位为一个字符，因此的确是去掉一个字符的时候，范围形状是长方形。再去掉一个字符，就又变成正方形。
不过如果你再仔细看的话，你会发现这个图示是以二进制区域编码为例子的，因为它每次扩大只是四倍，而不是32倍。32倍的图不好画。。
我看看让编辑在图示里加上说明优化一下吧。
-----------------------
老师，这里我在追问一下，在上一条下面评论怕你看不见：
也就是经度和纬度的字符交替的去掉吗？我看文中是连续去了最后的两个字母，也就是只操作了经度，纬度没变。还有就是下面Trie树是不是也不应该按照字母的顺序形成一个链了？也应该是经度，纬度交替的形成了？

展开




一步

2020-04-28

当前地址的 GeoHash 编码为 wx4g6yc8，这个根据上节学的编码规范，前4个字母代码纬度，后面四个代表经度，如果去掉最后一个字符不是代表纬度不变，经度的范围扩大 2 ^ 5 倍，这样的范围不应该是一个长方形吗？怎么会是图中的正方形呢？

展开

作者回复: 你看得很仔细。Geohash由于是5个比特位为一个字符，因此的确是去掉一个字符的时候，范围形状是长方形。再去掉一个字符，就又变成正方形。
不过如果你再仔细看的话，你会发现这个图示是以二进制区域编码为例子的，因为它每次扩大只是四倍，而不是32倍。32倍的图不好画。。
我看看让编辑在图示里加上说明优化一下吧。

 2


那时刻

2020-04-27

在四叉树从当前子节点去搜索附近子节点时，需要去到上层父节点。如果子节点以双向链表类似B+树，是否可行呢？

展开

作者回复: 你这个思考很好。四叉树能否使用b+树类似的双向链表呢？我来说说我的理解。
如果是满四叉树的话，那么我们可以将所有叶子节点使用双向链表连接起来。当我们查询到一个叶子节点不满足k个结果时，我们需要扩大范围，那么我们可以沿着左右两个方向去扩展。但是，我们是要扩展多少才OK呢？我们并不好判断新节点和当前节点的位置关系。你可以结合我文中的满四叉树的例子看看，如果查询到的节点是0110，其实离它最近的点可能是在1001区域中(见13讲中的区域编码图)，它需要往右边走三个元素才能到达这个节点。因此，遍历并无法判断当前节点和新扩展节点之间的关系。不如递归便捷。

而如果是非满四叉树的话，叶子节点不是一个层级的，并且节点还会分裂。进行链表管理会更加麻烦。




那时刻

2020-04-27

想到一种情况一个节点不一定生成四个叶子结点，比如某个城市的加油站都集中在某个小范围区域内，在上层节点看分裂子节点数量可能小于四。

展开

作者回复: 是的。极端情况就是所有插入的数据都属于一个小区域，那么根节点就不需要分裂出其他分叉了。




峰

2020-04-27

刚看到四叉树那段，就想着这不前缀树嘛，看到前缀树，想空间检索怎么能木有kd-tree，然后r-tree呢，我放心了，没有了哈哈哈。

以我的认知看，到了高维，先不是数据结构高效不高效的问题，先是高维诅咒引发的相似度不再有效问题，大家都很相似肿么搞，于是才有一帮人搞什么流形学习，在高维空间找低维表示，知识的世界就怎么无限延展开，我要老了=_=，哈哈哈，这个落点😜

最后回答下问题，这跟插入数据的分布情况有关，就比如根节点0011 0010 1001 1000，分裂，那根节点就可以多出两个二层节点00 10，然后一个节点指向0011 0010 ，另一个指向1001 1000，这种做法就偏b树的分裂方式，当然也可以优先对前缀最多的子节点集合进行分裂下推，都是动态分裂的策略问题，看你想达到什么效果，比如数据库b+树的分裂不会是两边子节点一样多，而是会让id 大的那边空一点，考虑的是id 经常是自增的，所以一般再有元素插入就在id 大的那边。

展开

作者回复: 哈哈，的确四叉树的这个用法和思路其实和前缀树很像。从这个角度来看，空间检索和字符串检索是有相似的地方的。
k-d树必须有，不过就像你说的，到了高维度以后，会有着无法精准检索的问题，因此许多高维度的相似检索问题都是使用近似最近邻检索方案来完成，而不是使用k-d树。这在后面会有介绍。




范闲

2020-04-27

四叉树最终分裂的时候不是4个节点，可能是因为数据分布造成的.假设有00 01 和10三类节点，如果00和01的数据量大，那分裂的时候可能就只有00和01.10被分到了01节点上

作者回复: 不会的哦。如果有10这个数据的话，那么它会是和01平行的独立一个分支，并不会合并到01中。
其实你在前面已经说出了正确答案了，就是“数据分布造成的，假设有00，01和10三类节点”。
你可以看这么一个例子，根节点阈值是4，目前只存有3个数据，分别属于00，01和10三个区域。如果再加一个00区域的数据，引发了根节点分裂，那么由于数据分布只在00，01和10三个区域上，因此只需要分裂出这三个叶子节点就好，并不需要分裂出11这个没有存任何数据的叶子节点。

 1



