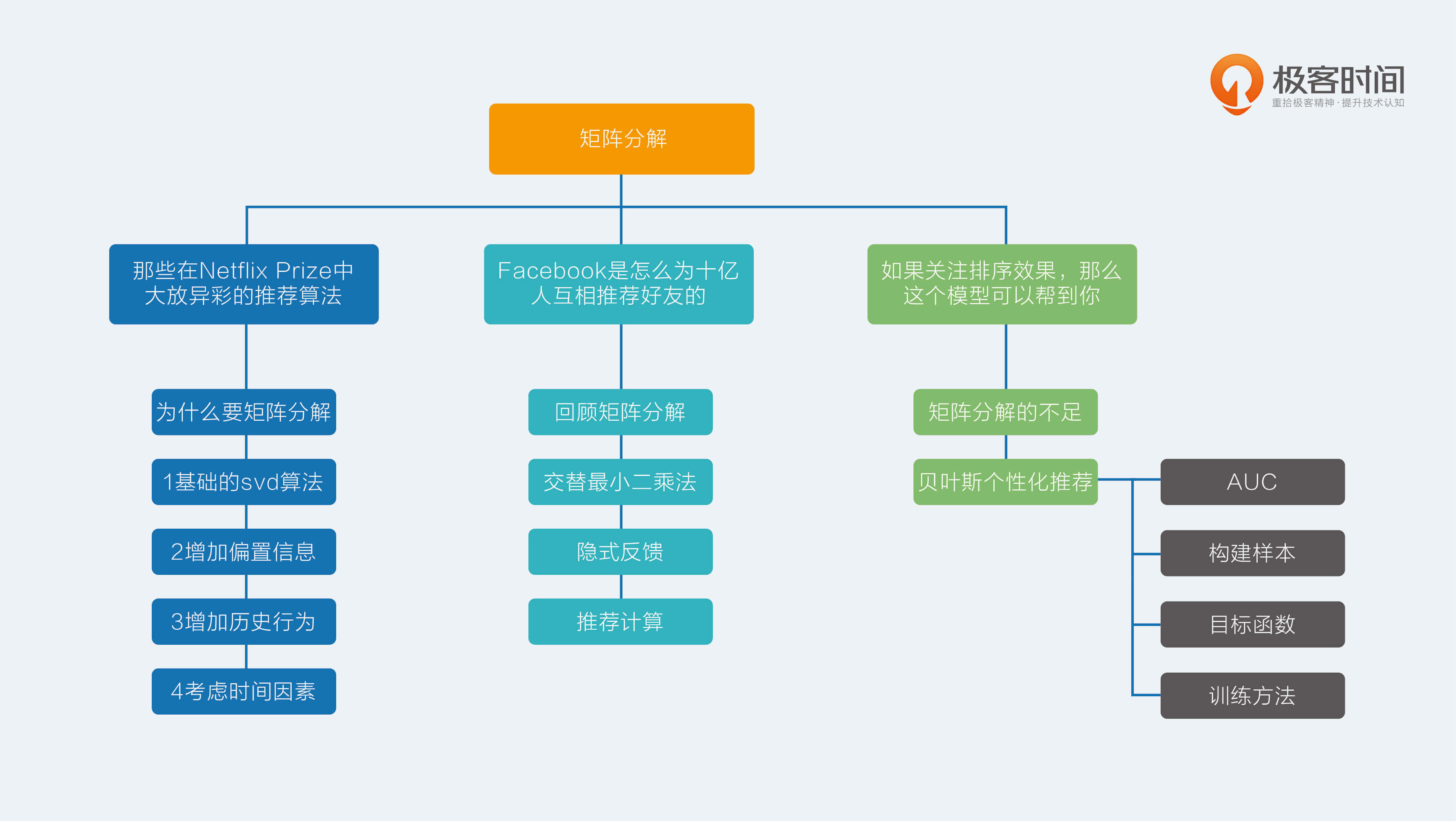
【矩阵分解】如果关注排序效果，那么这个模型可以帮到你

矩阵分解在推荐系统中的地位非常崇高，恐怕本专栏介绍的其他算法模型都不能轻易地撼动它。

它既有协同过滤的血统，又有机器学习的基因，可以说是非常优秀了；但即便如此，传统的矩阵分解无论是在处理显式反馈，还是处理隐式反馈都让人颇有微词，这一点是为什么呢？

矩阵分解的不足

前面我讲过的两种矩阵分解，本质上都是在预测用户对一个物品的偏好程度，哪怕不是预测评分， 只是预测隐式反馈，也难逃这个事实，因为算法展现出来的目标函数就出卖了这一切。

得到这样的矩阵分解结果后，常常在实际使用时，又是用这个预测结果来排序。所以，从业者们口口声声宣称想要模型的预测误差最小化，结果绕了一大圈最后还是只想要一个好点的排序，让人不禁感叹：人心总是难测。

这种针对单个用户对单个物品的偏好程度进行预测，得到结果后再排序的问题，在排序学习中的行话叫做 point-wise，其中 point 意思就是：只单独考虑每个物品，每个物品像是空间中孤立的点一样。

与之相对的，还有直接预测物品两两之间相对顺序的问题，就叫做 pair-wise，pair，顾名思义就是成对成双，也许恐怕这类模型对单身的人士不是很友好。

前面讲的矩阵分解都属于 point-wise 模型。这类模型的尴尬是：只能收集到正样本，没有负样本，于是认为缺失值就是负样本，再以预测误差为评判标准去使劲逼近这些样本。逼近正样本没问题，但是同时逼近的负样本只是缺失值而已，还不知道真正呈现在用户面前，到底是不喜欢还是喜欢呢？

虽然这些模型采取了一些措施来规避这个问题，比如负样本采样，但是尴尬还是存在的，为了排序而绕路也是事实。

既然如此，能不能直面问题，采用 pair-wise 来看待矩阵分解呢？当然能，不然我也不会写出这一篇专栏文章了。

其实人在面对选择时，总是倾向矮子中选高个子，而不是真的在意身高到底是不是 180，因此，更直接的推荐模型应该是：能够较好地为用户排列出更好的物品相对顺序，而非更精确的评分。

这个问题已经有可爱的从业者们提出了方法，就是本文的主角：贝叶斯个性化排序，简称 BPR 模型。下面，我就带你一探这个模型的究竟。

贝叶斯个性化排序

在前面的专栏文章中，有一个词叫做均方根误差，被我提过多次，用于评价模型预测精准程度的。那么现在要关注的是相对排序，用什么指标比较好呢？答案是 AUC，AUC 全称是 Area Under Curve，意思是曲线下的面积，这里的曲线就是 ROC 曲线。

AUC

但是，我不打算继续解释什么是 ROC 曲线了，那是它的原始定义，而我想跟你悄悄说的是另一件事，AUC 这个值在数学上等价于：模型把关心的那一类样本排在其他样本前面的概率。最大是 1，完美结果，而 0.5 就是随机排列，0 就是完美地全部排错。

听到这个等价的 AUC 解释，你是不是眼前一亮？这个非常适合用来评价模型的排序效果，比如说，得到一个推荐模型后，按照它计算的分数，能不能把用户真正想消费的物品排在前面？这在模型上线前是可以用日志完全计算出来的。

AUC 怎么计算呢？一般步骤如下。

1. 用模型给样本计算推荐分数，比如样本都是用户和物品这样一对一对的，同时还包含了有无反馈的标识；
2. 得到打过分的样本，每条样本保留两个信息，第一个是分数，第二个是 0 或者 1，1 表示用户消费过，是正样本，0 表示没有，是负样本；
3. 按照分数对样本重新排序，降序排列；
4. 给每一个样本赋一个排序值，第一位 r1 = n，第二位 r2 = n-1，以此类推；其中要注意，如果几个样本分数一样，需要将其排序值调整为他们的平均值；
5. 最终按照下面这个公式计算就可以得到 AUC 值。

我在文稿中放了这个公式，你可以点击查看。

这个公式看上去复杂，其实很简单，由两部分构成：

第一部分： 分母是所有我们关心的那类样本，也就是正样本，有 M 个，以及其他样本有 N 个，这两类样本相对排序总共的组合可能性，是 M x N；

第二部分： 分子也不复杂，原本是这样算的：第一名的排序值是 r1，它在排序上不但比过了所有的负样本，而且比过了自己以外的正样本。

但后者是自己人，所以组合数要排除，于是就有 n - M 种组合，以此类推，排序值为 rM 的就贡献了 rM - 1，把这些加起来就是分子。

关于 AUC，越接近 1 越好是肯定的，但是并不是越接近 0 就越差，最差的是接近 0.5，如果 AUC 很接近 0 的话，只需要把模型预测的结果加个负号就能让 AUC 接近 1，具体的原因自行体会。

好了，已经介绍完排序的评价指标了，该主角出场了，BPR 模型，它提出了一个优化准则和学习框架，使得原来传统的矩阵分解放进来能够焕发第二春。

那到底 BPR 做了什么事情呢？主要有三点：

1. 一个样本构造方法；
2. 一个模型目标函数；
3. 一个模型学习框架。

通过这套三板斧，便可以脱离评分预测，来做专门优化排序的矩阵分解。下面详细说说这三板斧。

构造样本

前面介绍的矩阵分解，在训练时候处理的样本是：用户、物品、反馈，这样的三元组形式。

其中反馈又包含真实反馈和缺失值，缺失值充当的是负样本职责。BPR 则不同，提出要关心的是物品之间对于用户的相对顺序，于是构造的样本是：用户、物品 1、物品 2、两个物品相对顺序，这样的四元组形式，其中，“两个物品的相对顺序”，取值是：

1. 如果物品 1 是消费过的，而物品 2 不是，那么相对顺序取值为 1，是正样本；
2. 如果物品 1 和物品 2 刚好相反，则是负样本；
3. 样本中不包含其他情况：物品 1 和物品 2 都是消费过的，或者都是没消费过的。

这样一来，学习的数据是反应用户偏好的相对顺序，而在使用时，面对的是所有用户还没消费过的物品，这些物品仍然可以在这样的模型下得到相对顺序，这就比三元组 point-wise 样本要直观得多。

目标函数

现在，每条样本包含的是两个物品，样本预测目标是两个物品的相对顺序。按照机器学习的套路，就该要上目标函数了。

要看 BPR 怎么完成矩阵分解，你依然需要像交替最小二乘那样的思想。

先假装矩阵分解结果已经有了，于是就计算出用户对于每个物品的推荐分数，只不过这个推荐分数可能并不满足均方根误差最小，而是满足物品相对排序最佳。

得到了用户和物品的推荐分数后，就可以计算四元组的样本中，物品 1 和物品 2 的分数差，这个分数可能是正数，也可能是负数，也可能是 0。

你和我当然都希望的情况是：如果物品 1 和物品 2 相对顺序为 1，那么希望两者分数之差是个正数，而且越大越好；如果物品 1 和物品 2 的相对顺序是 0，则希望分数之差是负数，且越小越好。

用个符号来表示这个差：Xu12，表示的是对用户 u，物品 1 和物品 2 的矩阵分解预测分数差。然后再用 sigmoid 函数把这个分数差压缩到 0 到 1 之间。

也其实就是用这种方式预测了物品 1 排在物品 2 前面的似然概率，所以最大化交叉熵就是目标函数了。

目标函数通常还要防止过拟合，加上正则项，正则项其实认为模型参数还有个先验概率，这是贝叶斯学派的观点，也是 BPR 这个名字中“贝叶斯”的来历。

BPR 认为模型的先验概率符合正态分布，对应到正则化方法就是 L2 正则，这些都属于机器学习的内容，这里不展开讲。

我来把目标函数写一下：

所有样本都计算：模型参数先验概率 p theta，和似然概率的乘积，最大化这个目标函数就能够得到分解后的矩阵参数，其中 theta 就是分解后的矩阵参数。

最后说一句，把这个目标函数化简和变形后，和把 AUC 当成目标函数是非常相似的，也正因为如此，BPR 模型的作者敢于宣称该模型是为 AUC 而生的。

训练方法

有了目标函数之后，就要有请训练方法了。显然是老当益壮的梯度下降可以承担这件事，梯度下降又有批量梯度和随机梯度下降两个选择，前者收敛慢，后者训练快却不稳定。因此 BPR 的作者使用了一个介于两者之间的训练方法，结合重复抽样的梯度下降。具体来说是这样做的：

1. 从全量样本中有放回地随机抽取一部分样本；
2. 用这部分样本，采用随机梯度下降优化目标函数，更新模型参数；
3. 重复步骤 1，直到满足停止条件。

这样，就得到了一个更符合推荐排序要求的矩阵分解模型了。

总结

今天是矩阵分解三篇的最后一篇，传统的矩阵分解，无论是隐式反馈还是显式反馈，都是希望更加精准地预测用户对单个物品的偏好，而实际上，如果能够预测用户对物品之间的相对偏好，则更加符合实际需求的直觉。

BPR 就是这样一整套针对排序的推荐算法，它事实上提出了一个优化准则和一个学习框架，至于其中优化的对象是不是矩阵分解并不是它的重点。

但我在这里结合矩阵分解对其做了讲解，同时还介绍了排序时最常用的评价指标 AUC 及其计算方法。

你在看了 BPR 算法针对矩阵分解的推荐计算过程之后，试着想一想，如果不是矩阵分解，而是近邻模型，那该怎么做？欢迎留言给我，一起聊聊。